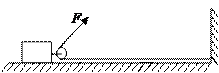如图所示为我国“嫦娥一号”卫星从发射到进入月球工作轨道的过程示意图．在发射过程中，经过一系列的加速和变轨，卫星沿绕地球“48小时轨道”在抵达近地点P时，主发动机启动，“嫦娥一号”卫星的速度在很短时间内由v1提高到v2，进入“地月转移轨道”，开始了从地球向月球的飞越．“嫦娥一号”卫星在“地月转移轨道”上经过114小时飞行到达近月点Q时，需要及时制动，使其成为月球卫星．之后，又在绕月球轨道上的近月点Q经过两次制动，最终进入绕月球的圆形工作轨道I．已知“嫦娥一号”卫星质量为m0，在绕月球的圆形工作轨道I上运动的周期为T，月球的半径r月，月球的质量为m月，万有引力恒量为G．
 |
（1）求卫星从“48小时轨道”的近地点P进入”地月转移轨道”过程中主发动机对“嫦娥一号”卫星做的功（不计地球引力做功和卫星质量变化）；
（2）求“嫦娥一号”卫星在绕月球圆形工作轨道I运动时距月球表面的高度；
（3）理论证明，质量为m的物体由距月球无限远处无初速释放，它在月球引力的作用下运动至距月球中心为r处的过程中，月球引力对物体所做的功可表示为W= G
．为使“嫦娥一号”卫星在近月点Q进行第一次制动后能成为月球的卫星，且与月球表面的距离不小于圆形工作轨道I的高度，最终进入圆形工作轨道，其第一次制动后的速度大小应满足什么条件？
如图所示，小滑块从斜面顶点A由静止滑至水平部分C点而停止。已知斜面高为h，滑块运动的整个水平距离为s，设转角B处无动能损失，斜面和水平部分与小滑块的动摩擦因数相同，求此动摩擦因数。
如图所示，斜面倾角为
，长为L，AB段光滑，BC段粗糙，且BC="2" AB。质量为m的木块从斜面顶端无初速下滑，到达C端时速度刚好减小到零。求物体和斜面BC段间的动摩擦因数μ。
如图所示，AB为1/4圆弧轨道，半径为R=0.8m，BC是水平轨道，长S=3m，BC处的摩擦系数为μ=1/15，今有质量m=1kg的物体，自A点从静止起下滑到C点刚好停止。求物体在轨道AB段所受的阻力对物体做的功。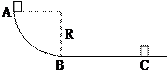
汽车发动机额定功率为60 kW，汽车质量为5.0×103 kg，汽车在水平路面行驶时，受到的阻力大小是车重的0.1倍，试求：汽车保持额定功率从静止出发后能达到的最大速度是多少？
如图所示，恒定的拉力大小F=8N，方向与水平线夹θ=60°角，拉着绳头使物体沿水平面移动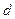
=2m的过程中，拉力做了多少功？