一支车队有15辆车，某天依次出发执行运输任务．第一辆车于下午2时出发，第二辆车于下午２时10分出发，第三辆车于下午2时20分出发，依此类推．假设所有的司机都连续开车，并都在下午6时停下来休息．
（１） 到下午6时，最后一辆车行驶了多长时间？
（２） 如果每辆车的行驶速度都是60km/h，这个车队当天一共行驶了多少km?
函数
（
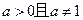）在区间
上减函数，求实数
的取值范围？
（1）求
的定义域；
（2）求使
成立的
的取值范围。
（1）求： A∪B，CR(A∩B)；
（2）若集合
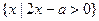,满足
，求实数
的取值范围
（1）若
,求函数
的零点；
（2）在（2）条件下证明: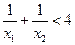
|
… |
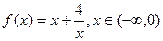
-0.5 |
-1 |
-1.5 |
-1.7 |
-1.9 |
-2 |
-2.1 |
-2.2 |
-2.3 |
-3 |
-4 |
… |
 |
… |
-8.5 |
-5 |
-4.17 |
-4.05 |
-4.005 |
-4 |
-4.005 |
-4.02 |
-4.04 |
-4.3 |
-5 |
… |
请观察表中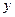
值随值变化的特点，完成以下的问题.
函数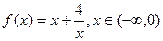在区间
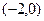上递减；
（1）证明：函数
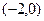在区间递减.
（2）思考：函数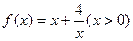
有最大值或最小值吗？如有，是多少？此时为何值？（直接回答结果，不需证明）