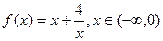

 |
… |
-0.5 |
-1 |
-1.5 |
-1.7 |
-1.9 |
-2 |
-2.1 |
-2.2 |
-2.3 |
-3 |
-4 |
… |
 |
… |
-8.5 |
-5 |
-4.17 |
-4.05 |
-4.005 |
-4 |
-4.005 |
-4.02 |
-4.04 |
-4.3 |
-5 |
… |
请观察表中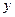 值随
值随 值变化的特点,完成以下的问题.
值变化的特点,完成以下的问题.
函数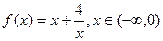 在区间
在区间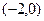 上递减;
上递减;
(1)证明:函数 在区间
在区间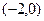 递减.
递减.
(2)思考:函数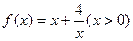 有最大值或最小值吗?如有,是多少?此时
有最大值或最小值吗?如有,是多少?此时 为何值?(直接回答结果,不需证明)
为何值?(直接回答结果,不需证明)
求与椭圆 有共同焦点,且过点
有共同焦点,且过点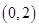 的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率。
的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率。
在△ABC中,已知角A、B、C所对的三条边分别是a、b、c且满足b2=ac.
求证:0<B≤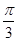 ;(2)求函数y=
;(2)求函数y=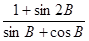 的值域.
的值域.
已知抛物线D的顶点是椭圆Q: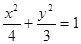 的中心O,焦点与椭圆Q的右焦点重合,点
的中心O,焦点与椭圆Q的右焦点重合,点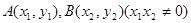 是抛物线D上的两个动点,且
是抛物线D上的两个动点,且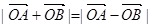
(1)求抛物线D的方程及y1y2的值;
(2)求线段AB中点轨迹E的方程;
(3)在曲线E上寻找一点,使得该点与直线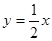 的距离最近.
的距离最近.
如图所示,在直三棱柱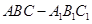 中,
中, ,
,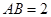 ,
,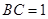 ,
, ,
, 是棱
是棱 的中点.
的中点.
(1)证明: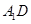
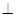 平面
平面 ;
;
(2)求二面角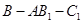 的余弦值.
的余弦值.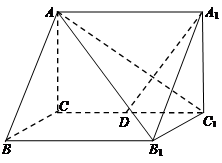
已知函数
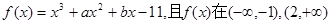 上单调递增,在(-1,2)上单调递减,又函数
上单调递增,在(-1,2)上单调递减,又函数 .
.
(1)求函数 的解析式;
的解析式;
(2)求证当