如图所示，有一电子束从a点处以一定的水平速度飞向竖直放置的荧光屏，并垂直击中荧光屏上的b点.已知电子的质量为m，电量为e.
若在电子束运行途中加一个仅存在于半径为r的圆形区域内的匀强磁场，磁感应强度为B，方向垂直纸面向里，圆心O在点a、b连线上，点O距荧光屏的距离为L。
（1）为使电子束仍击中荧光屏上的点b，可加一场强为E的匀强电场.指出此匀强电场的方向和范围，并求出电子束的速度。
（2）现撤去电场，电子束仍以原速度大小沿水平方向从a点发射，试求出此时侧移量y
的表达式。
如图所示,横截面是直角三角形ABC的三棱镜对红光的折射率为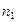
,对紫光的折射率为
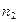.一束很细的白光由棱镜的一个侧面AB垂直射入,从另一个侧面AC折射出来.已知棱镜的顶角∠A=30°,AC边平行于光屏MN,且与光屏的距离为L.求在光屏上得到的可见光谱的宽度.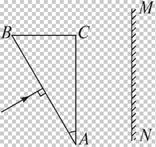
如图所示，用折射率n=2的透明材料做的空心球，内、外半径分别为a和b.内球面上涂一层能完全吸收光的物质，则当被一束平行光照射时，被吸收掉的光束截面面积为多大？
一路灯距地面的高度为h,身高为l的人以速度v匀速行走,如图所示.
(1)试证明人的头顶的影子做匀速运动;
(2)求人影的长度随时间的变化率.
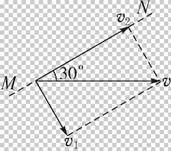
如图所示,S为一在xOy平面内的点光源.一平面镜垂直于xOy平面放置,它与xOy平面的交线为MN,MN与x轴的夹角θ=30°.现保持S不动,令平面镜MN以速度v沿x轴正方向运动,则S经平面镜所成的像以多大速度沿什么方向运动?
太阳与月球的直径分别为1.39×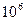
km和3.5×
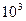km.设日全食时太阳到地面的距离为1.5×
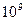km,月球到地面的距离为3.8×
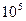km,试计算地面上能见到日全食区域的面积(可把该区域的地面视为平面).