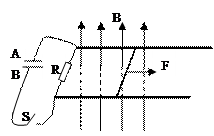
喷墨打印机的原理示意图如图所示，其中墨盒可以发出墨汁液滴，此液滴经过带电室时被带上负电，带电多少由计算机按字体笔画高低位置输入信号加以控制．带电后液滴以一定的初速度进入偏转电场，带电液滴经过偏转电场发生偏转后打到纸上，显示出字体．计算机无信号输入时，墨汁液滴不带电，径直通过偏转板最后注入回流槽流回墨盒．
设偏转极板长L1="1.6" cm，两板间的距离d="0.50" cm,两板间的电压U=8.0×103 V，偏转极板的右端距纸的距离L2="3.2" cm．若一个墨汁液滴的质量m=1.6×10-10 kg,墨汁液滴以v0="20" m/s的初速度垂直电场方向进入偏转电场，此液滴打到纸上的点距原入射方向的距离为2. 0 mm．不计空气阻力和重力作用．求：这个液滴通过带电室后所带的电量q．
如图所示，一束具有各种速率的两种质量数不同的一价铜离子，水平地经过小孔S1射入垂直的匀强电场和匀强磁场区域，已知匀强电场的场强E="1X" l05v/m，匀强磁场的磁感应强度为Bl=0.4T．求：
(1)速度多大的一价铜离子，才能通过与Sl小孔正对的S2小孔射入另一匀强磁场B2中?
(2)如果这些一价铜离子在匀强磁场B2中发生偏转后，打在过小孔S2且与两磁场分界面重合的照相底片上，已知分界面与小孔SlS2连线垂直，若感光点到小孔S2的距离分别为d1=0.654m,d2="0.674m" ,那么对应的两种铜离子的质量数之比为多大? 
如图所示，光滑水平面上有一长板车，车的上表面0A段是一长为己的水平粗糙轨道，A的右侧光滑，水平轨道左侧是一光滑斜面轨道，斜面轨道与水平轨道在O点平滑连接。车右端固定一个处于锁定状态的压缩轻弹簧，其弹性势能为Ep，一质量为m的小物体(可视为质点)紧靠弹簧，小物体与粗糙水平轨道间的动摩擦因数为μ，整个装置处于静止状态。现将轻弹簧解除锁定，小物体被弹出后滑上水平粗糙轨道。车的质量为 2m，斜面轨道的长度足够长，忽略小物体运动经过O点处产生的机械能损失，不计空气阻力。求：
(1)解除锁定结束后小物体获得的最大动能；
(2)当μ满足什么条件小物体能滑到斜面轨道上，满足此条件时小物体能上升的最大高度为多少?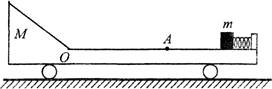
如图所示，一对平行放置的金属板M、N的中心各有一小孔P、Q，PQ连线垂直金属板；N板右侧的圆形区域A内分布有方向垂直于纸面向外的匀强磁场，磁感应强度大小为B，圆半径为r，且圆心O在PQ的延长线上，两平行金属板与匝数为n，边长为a的正方形线圈相连，现有垂直于线圈平面均匀增大的磁场，磁感应强度变化率为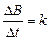
，一质量为m、电量为q的带负电粒子（重力不计），初速度为零，从P点进入两板间，求：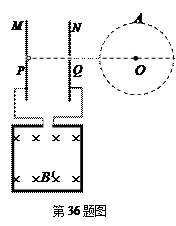
（1）两平行板之间的电势差
（2）粒子从Q点射出时的速度
（3）带电粒子通过该圆形磁场的偏转角θ
如图所示，光滑的水平导轨MN右端N处与水平传送带理想连接，传送带长度L=0.8m，皮带以恒定速率v=3.0m/s向右匀速运动。传送带的右端处平滑连接着一个在竖直平面内、半径为R=0.4m的光滑半圆轨道PQ，两个质量均为m=0.2kg的滑块A、B置于水平导轨MN上，开始时滑块A、B之间用细绳相连，其间有一压缩的轻弹簧，系统处于静止状态。现使细绳断开，弹簧伸展，滑块B脱离弹簧后滑上传送带，从右端滑出并沿半圆轨道运动到最高点Q后水平飞出，又正好落回N点。已知滑块B与传送带之间的动摩擦因数μ=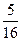
，取g=10m／s2。求：
（1）滑块B到达Q点时速度的大小；
（2）滑块B在半圆轨道P处对轨道的压力；
（3）压缩的轻弹簧的弹性势能Ep。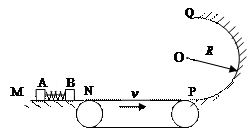
如图所示，导体棒长Ｌ=0.2m、电阻r=0.1Ω，放在位于水平面内间距也为L光滑无限长的平行金属导轨上，两导轨左端接一负载电阻R＝0.4Ω和一个C＝2×10-10F的电容器。一匀强磁场B=0.5T，方向垂直于导轨所在平面向上。开始时开关S断开，导体棒在一个平行于导轨的恒定外力F=0.10Ｎ作用下匀速向右运动，导轨电阻忽略。
（1）求棒匀速运动时的速度；
（2）若开关S闭合，达到稳定后，求电容器的带电量，指出A板带何种电荷。