如图所示,光滑水平面上有一长板车,车的上表面0A段是一长为己的水平粗 糙轨道,A的右侧光滑,水平轨道左侧是一光滑斜面轨道,斜面轨道与水平轨道在O点平 滑连接。车右端固定一个处于锁定状态的压缩轻弹簧,其弹性势能为Ep,一质量为m的小物体(可视为质点)紧靠弹簧,小物体与粗糙水平轨道间的动摩擦因数为μ,整个装置处于静止状态。现将轻弹簧解除锁定,小物体被弹出后滑上水平粗糙轨道。车的质量为 2m,斜面轨道的长度足够长,忽略小物体运动经过O点处产生的机械能损失,不计空气阻力。求:
(1)解除锁定结束后小物体获得的最大动能;
(2)当μ满足什么条件小物体能滑到斜面轨道上,满足此条件时小物体能上升的最大高度为多少?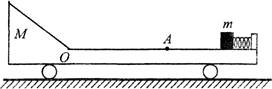
如图所示,质量为m的由绝缘材料制成的球与质量为M=19m的金属球并排悬挂。现将绝缘球拉至与竖直方向成θ=60°的位置自由释放,下摆后在最低点处与金属球发生弹性碰撞。在平衡位置附近存在垂直于纸面的磁场。已知由于磁场的阻尼作用,金属球将于再次碰撞前停在最低点处。求经过几次碰撞后绝缘求偏离竖直方向的最大角度将小于45°。
在光滑的水平面上,质量为m1的小球A以速率v0向右运动。在小球的前方O点处有一质量为m2的小球B处于静止状态,如图所示。小球A与小球B发生正碰后小球A、B均向右运动。小球B被在Q点处的墙壁弹回后与小球A在P点相遇,PQ=1.5PO。假设小球间的碰撞及小球与墙壁之间的碰撞都是弹性的,求两小球质量之比m1∶m2。
如图所示,质量mA为4.0kg的木板A放在水平面C上,木板与水平面间的动摩擦因数μ为0.24,木板右端放着质量mB为1.0kg的小物块B(视为质点),它们均处于静止状态.木板突然受到水平向右的12N·s的瞬时冲量作用开始运动,当小物块滑离木板时,木板的动能EKA为8.0J,小物块的动能EKB为0.50J,重力加速度取10m/s2,求:
(1)瞬时冲量作用结束时木板的速度υ0;
(2)木板的长度L.
如图所示,C是放在光滑的水平面上的一块木板,木板的质量为3m,在木板的上面有两块质量均为m的小木块A和B,它们与木板间的动摩擦因数均为μ。最初木板静止,A、B两木块同时以方向水平向右的初速度V0和2V0在木板上滑动,木板足够长, A、B始终未滑离木板。求:
(1)木块B从刚开始运动到与木板C速度刚好相等的过程中,木块B所发生的位移;
(2)木块A在整个过程中的最小速度。
甲、乙两小孩各乘一辆小车在光滑水平面上匀速相向行驶,速度均为6m/s。甲车上有质量为m=1kg的小球若干个,甲和他的车及所带小球的总质量为M1=50kg,乙和他的车总质量为M2=30kg。现为避免相撞,甲不断地将小球以相对地面16.5m/s的水平速度抛向乙,且被乙接住。假设某一次甲将小球抛出且被乙接住后刚好可保证两车不致相撞,试求此时:
(1)两车的共同速度为多少?(2)甲总共抛出了多少个小球?