据1951年，物理学家发现了"电子偶数"，所谓"电子偶数"就是由一个负电子和一个正电子绕它们连线的中点旋转形成的相对稳定的系统．已知正、负电子的质量均为m，普朗克常量为h，静电常量为k.
(1)若正、负电子是由一个光子和核场作用产生的，且相互作用过程中核场不提供能量，则此光子的报率必须大于某个临界值，此临界值为多大？
(2)假设"电子偶数"中，正负电子绕它们连线的中点做匀速圆周运动的轨道半径r、运动速度v及电子质量满足波尔的轨道量子化理论：
．"电子偶数"的能量为正、负电子运动的动能和系统的电势能之和，已知两正、负电子相距L时系统的电势能为
．试求n=1时"电子偶数"的能量.
(3)"电子偶数"由第一激发态跃迁到基态发出的光子的波长为多大？
如图所示，一质量为m的砂袋用长为l的绳子拴住悬挂在O点，被拳击运动员水平击中后，荡起的最大高度是h.求砂袋刚被击中后的瞬间，砂袋的向心加速度是多大?
如图所示，直径为d的纸制圆筒以角速度ω绕垂直纸面的轴O匀速运动（图示为截面）。从枪口发射的子弹沿直径穿过圆筒。若子弹在圆筒旋转不到半周时，在圆周上留下a、b两个弹孔，已知aO与bO夹角为θ，求子弹的速度。
如图所示是生产流水线上的皮带传输装置，传输带上等间距地放着很多半成品产品。A轮处装有光电计数器，它可以记录通过A处的产品数目。已知测得轮A、B的半径分别为rA=20cm，rB=l0cm，相邻两产品距离为30cm，lmin内有41个产品通过A处，求：
（1）产品随传输带移动的速度大小；
（2）A、B轮轮缘上的两点P、Q及A轮半径中点M的线速度和角速度大小，并在图中画出线速度方向；
（3）如果A轮是通过摩擦带动C轮转动，且rC="5" cm，在图中描出C轮的转动方向，求出C轮的角速度（假设轮不打滑）。
一半径为R的雨伞绕柄以角速度ω匀速旋转，如图所示，伞边缘距地面高h，甩出的水滴在地面上形成一个圆，求此圆半径r为多少?
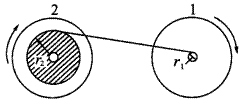
如图所示为录音机在工作时的示意图，轮子1是主动轮，轮子2为从动轮，轮1和轮2就是磁带盒内的两个转盘，空带一边半径为r1="0.5" cm，满带一边半径为r2=3cm，已知主动轮转速不变，恒为nl=36r／min，试求：
（1）从动轮2的转速变化范围；
（2）磁带运动的速度变化范围。