如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π。
(Ⅰ)求证:AF⊥BD;
(Ⅱ)求二面角A―BD―E的正弦值。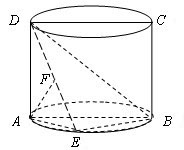
(本小题满分12分)设函数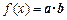 ,其中向量
,其中向量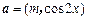 ,
,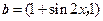 ,
,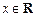 ,且
,且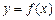 的图象经过点
的图象经过点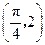 .
.
(Ⅰ)求实数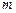 的值;
的值;
(Ⅱ)求函数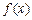 的最小值及此时
的最小值及此时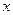 值的集合.
值的集合.
(本小题满分12分)设函数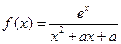 ,其中
,其中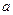 为实数.
为实数.
(I)若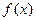 的定义域为
的定义域为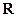 ,求
,求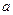 的取值范围;
的取值范围;
(II)当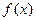 的定义域为
的定义域为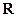 时,求
时,求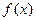 的单调减区间.
的单调减区间.
(本小题满分12分)某项选拔共有三轮考核,每轮设有一问题,能正确回答问题者进入下一轮考核,否则即被淘汰.已知某选手能正确回答第一、二、三、轮的问题的概率分别为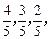 且各轮问题能否正确回答互不影响.
且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在选择中回答问题的个数记为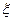 ,求随机变量
,求随机变量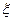 的分布列与数学期望.(注:本小题结果可用分数表示)
的分布列与数学期望.(注:本小题结果可用分数表示)
已知数列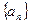 是等差数列,
是等差数列,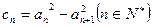
(1)判断数列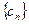 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;
(2)如果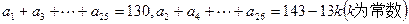 ,试写出数列
,试写出数列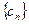 的通项公式;
的通项公式;
(3)在(2)的条件下,若数列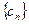 得前n项和为
得前n项和为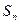 ,问是否存在这样的实数
,问是否存在这样的实数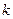 ,使
,使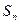 当且仅当
当且仅当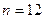 时取得最大值。若存在,求出
时取得最大值。若存在,求出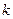 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
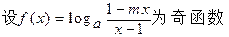 ,
,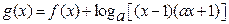 ( a>1,且
( a>1,且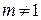 )
)
(1) 求m 值 ,
(2) 求g(x)的定义域;
(3) 若g(x)在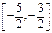 上恒正,求a的取值范围。
上恒正,求a的取值范围。