设数列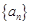 的前
的前 项和为
项和为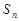 ,若对任意
,若对任意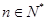 ,都有
,都有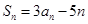 .
.
⑴求数列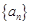 的首项;
的首项;
⑵求证:数列 是等比数列,并求数列
是等比数列,并求数列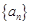 的通项公式;
的通项公式;
⑶数列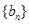 满足
满足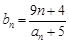 ,问是否存在
,问是否存在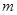 ,使得
,使得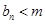 恒成立?如果存在,求出
恒成立?如果存在,求出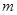 的值,如果不存在,说明理由.
的值,如果不存在,说明理由.
(本小题满分12分)已知△ABC的面积S满足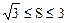 , 且
, 且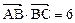 ,
, 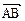 与
与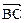 的夹角为
的夹角为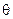 .
.
(I) 求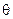 的取值范围;
的取值范围;
(II)求函数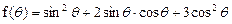 的最小值.
的最小值.
(本小题满分12分)等比数列{an}的各项均为正数,且2a1+3a2=1,a=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列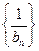 的前n项和.
的前n项和.
(本小题满分12分)数学试题中共有10道选择题,每道选择题都有4个选项,其中有且仅有一个是正确的,评分标准规定:“每题只选1项,答对得5分,不答或答错得0分”,某考生每道题都给出了一个答案,已确定有6道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:
(1)得50分的概率;
(2)得多少分的可能性最大?
(本小题满分12分)已知条件 (a>0)和条件
(a>0)和条件 ,
,
请选取适当的实数 的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题.则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题.则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
(本小题满分14分)对于函数 ,若存在
,若存在 ,使
,使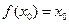 成立,则称
成立,则称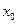 为
为 的不动点。如果函数
的不动点。如果函数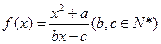 有且仅有两个不动点
有且仅有两个不动点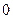 、
、 ,且
,且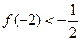 。
。
(1)试求函数 的单调区间;
的单调区间;
(2)已知各项均为负的数列 满足
满足 ,求证:
,求证: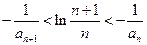 ;
;
(3)设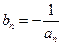 ,
,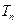 为数列
为数列 的前
的前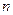 项和,求证:
项和,求证: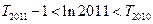 。
。