(本小题满分12分)某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗 原料1千克、
原料1千克、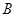 原料2千克;生产乙产品1桶需耗
原料2千克;生产乙产品1桶需耗 原料2千克,
原料2千克,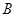 原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗
原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗 、
、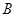 原料都不超过12千克.如何合理安排生产计划 ,使公司可获得最大利润?最大利润为多少?
原料都不超过12千克.如何合理安排生产计划 ,使公司可获得最大利润?最大利润为多少?
(本小题满分14分)在平面直角坐标系 中,不共线的四点
中,不共线的四点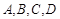 满足
满足 且
且
(1)求向量 的坐标;
的坐标;
(2)求四边形 的面积
的面积
(本小题满分14分)已知函数 ,若函数
,若函数 在点
在点 处的切线与直线
处的切线与直线 相互垂直.
相互垂直.
(1)求 的值.
的值.
(2)求函数 的最大值.
的最大值.
(3)证明:对于任意的 ,都有
,都有 成立.
成立.
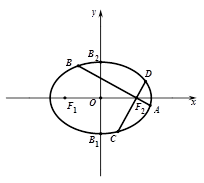
(本小题满分14分)如图所示,椭圆 的左右焦点分别为
的左右焦点分别为 ,点
,点 为椭圆
为椭圆 与坐标轴的交点,其中
与坐标轴的交点,其中 面积为
面积为 ,且椭圆
,且椭圆 的离心率为
的离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)过椭圆 的右焦点
的右焦点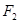 作两条相互垂直的弦
作两条相互垂直的弦 ,求由
,求由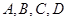 四点构成的四边形的面积的取值范围.
四点构成的四边形的面积的取值范围.
(本小题满分14分)设正数数列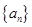 的前n项和为
的前n项和为 ,
,
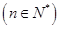 .
.
(1)求证: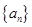 是等差数列;
是等差数列;
(2)设 为数列{
为数列{ }的前n项和,求
}的前n项和,求 ;
;
(3)设 ,证明:
,证明: 
(本小题满分14分)如图所示,平面
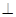 平面
平面 ,且四边形
,且四边形 为正方形,
为正方形, ,
, ∥
∥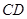 ,
, ,
, 为
为 的中点.
的中点.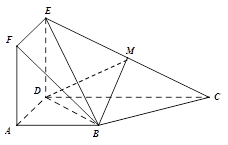
(1)求证: ∥平面
∥平面 ;
;
(2)求证: 平面
平面 ;
;
(3)求三棱锥 的体积.
的体积.