设向量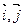 为直角坐标平面内x轴,y轴正方向上的单位向量.若向量
为直角坐标平面内x轴,y轴正方向上的单位向量.若向量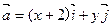 ,
,
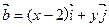 ,且
,且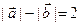 .
.
(1)求满足上述条件的点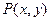 的轨迹方程;
的轨迹方程;
(2)设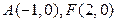 ,问是否存在常数
,问是否存在常数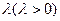 ,使得
,使得 恒成立?证明你的结论.
恒成立?证明你的结论.
在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC,AB=2EF.若M是线段AD的中点,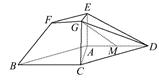
求证:GM∥平面ABFE.
如图,在正方体ABCD-A1B1C1D1中,E,F,G,M,N分别是B1C1,A1D1,A1B1,BD,B1C的中点,
求证:(1)MN∥平面CDD1C1.
(2)平面EBD∥平面FGA.
在四棱锥P -ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为60°.
(1)求四棱锥的体积.
(2)若E是PB的中点,求异面直线DE与PA所成角的余弦值.
直三棱柱ABC-A1B1C1的底面为等腰直角三角形,∠BAC=90°,AB=AC=2,AA1=2 ,E,F分别是BC,AA1的中点.
,E,F分别是BC,AA1的中点.
求(1)异面直线EF和A1B所成的角.
(2)三棱锥A-EFC的体积.
如图,在四面体ABCD中作截面PQR,若PQ,CB的延长线交于M,RQ,DB的延长线交于N,RP,DC的延长线交于K,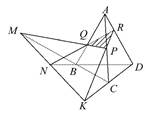
求证:M,N,K三点共线.