（1）有关热辐射和光的本性，请完成下列填空题
黑体辐射的规律不能用经典电磁学理论来解释，1900年德国物理学家普朗克认为能量是由一份一份不可分割最小能量值组成，每一份称为_________.1905年爱因斯坦从此得到启发，提出了光子的观点，认为光子是组成光的最小能量单位，光子的能量表达式为_________，并成功解释了__________________现象中有关极限频率、最大初动能等规律，写出了著名的______________方程，并因此获得诺贝尔物理学奖。
（2）已知氘核质量2.0136u，中子质量为1.0087u，
核质量为3.0150u。
A、写出两个氘核聚变成的核反应方程___________________________________。
B、计算上述核反应中释放的核能。（结果保留2位有效数字）（1u=931.5Mev）
C、若两氘以相等的动能0.35MeV作对心碰撞即可发生上述核反应，且释放的核能全部转化为机械能，则反应中生成的核和中子的动能各是多少？（结果保留2位有效数字）
如图所示，质量为M，长为L的小车静止在光滑水平面上，小车最右端固定有一个百度不计的竖直挡板，另有一质量为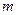
的小物体以水平向右的初速度
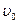从小车最左端出发，运动过程中与小车右端的挡板发生无机械能损失的碰撞，碰后小物体恰好停在小车的最左端。求：
（1）小物体停在小车的最左端时小车的速度多大？
（2）小物体与小车间的动摩擦因数多大？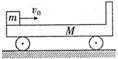
如图，在水平面上有两条平行导电导轨MN、PQ，导轨间距离为l，匀强磁场垂直于导轨所在的平面（纸面）向里，磁感应强度的大小为B，两根金属杆1、2摆在导轨上，与导轨垂直，它们的质量和电阻分别为
、
和
、
，两杆与导轨接触良好，与导轨间的动摩擦因数都为
，已知：杆1被外力拖动，以恒定的速度
沿导轨运动，达到稳定状态时，杆2也以恒定速度沿导轨运动，导轨的电阻可忽略，求此时杆2的动量大小。
将质量
的物体在离水平地面
高处以初速度
m/s水平抛出，物体受到跟
同方向的恒定风力F=5N作用，g取
。求：物体的水平射程。
如图所示，一个质量为
、电荷量
带正电的小球，用绝缘细线悬于竖直放置的足够大的平行金属板中的O点，已知两板相距
。合上开关后，小球静止时细线与竖直方向的夹角为
，电源电动势
，内阻
，电阻
，
。G取
。求：
（1）通过电源的电流强度；
（2）夹角的大小。
“神舟”七号飞船于2008年9月25日晚9时10分从酒泉卫星发射中心发射升空。飞船在太空预定轨道绕地球飞行了四十六圈。飞行期间，航天员飞行乘组在地面组织指挥和测控系统的协同配合下，顺利完成了空间出舱活动和一系列空间科学试验。28日17时37分， “神舟”七号飞船在内蒙古中部预定区域成功着陆。随后，执行飞行任务的航天员翟志刚、刘伯明和景海鹏安全出舱，中国神舟七号载人航天飞行获得圆满成功。飞船升空后，首先沿椭圆轨道运行，近地点约为200公里，远地点约为347公里。在绕地球飞行5圈后，地面发出指令，使飞船上的发动机在飞船到达远地点时自动点火，实行变轨，提高了飞船的速度，使得飞船在距地面343公里的圆轨道上飞行。（设地球半径为R，地面的重力加速度为g ）
（1）试分析航天员在舱内“漂浮起来 ”的现象产生的原因。
（2）“神舟七号”飞船在绕地飞行5圈后进行变轨，由原来的椭圆轨道变为距地面高为h 的圆形轨道。则飞船在上述圆形轨道运行的周期是多少？（用h、R、g表示）
（3）返回舱在将要着陆之前，由于空气阻力作用有一段匀速下落过程，若空气阻力与速度的平方成正比，比例系数为k，返回舱的质量为m，且匀速下降过程的重力加速度为
，则此过程中返回舱的速度？以及匀速下降过程中单位时间内转化为内能的机械能为多少？