一束白光从玻璃里射入稀薄空气中,已知玻璃的折射率为1.53,求入射角为下列两种情况时,光线的折射角各为多少?
(1)入射角为50°;
(2)入射角为30°。
一个带正电的微粒,从A点射入水平方向的匀强电场中,微粒沿直线AB运动,如图所示,AB与电场线夹角θ=30°,已知带电微粒的质量 ,电量
,电量 ,A、B相距
,A、B相距 。(取g=10m/s2,结果保留二位有效数字)求:
。(取g=10m/s2,结果保留二位有效数字)求: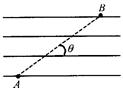
(1)说明微粒在电场中运动的性质,要求说明理由。
(2)电场强度的大小和方向?
(3)要使微粒从A点运动到B点,微粒射入电场时的最小速度是多少?
如图所示,在 的空间中,存在沿
的空间中,存在沿 轴方向的匀强电场
轴方向的匀强电场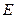 ;在
;在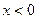 的空间中,存在沿
的空间中,存在沿 轴负方向的匀强电场,场强大小也为
轴负方向的匀强电场,场强大小也为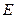 。一电子
。一电子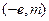 在
在 处的P点以沿
处的P点以沿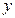 轴正方向的初速度v0开始运动,不计电子重力。求:
轴正方向的初速度v0开始运动,不计电子重力。求: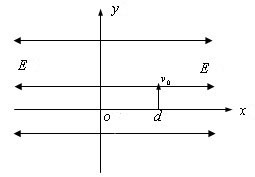
(1)电子的 方向分运动的周期。
方向分运动的周期。
(2)电子运动的轨迹与y轴的各个交点中,任意两个交点的距离。
如图所示,两块长3cm的平行金属板AB相距1cm,并与300V直流电源的两极相连接,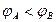 ,如果在两板正中间有一电子(m=9×10-31kg,e=-1.6×10-19C),沿着垂直于电场线方向以2×107m/s的速度飞入,则
,如果在两板正中间有一电子(m=9×10-31kg,e=-1.6×10-19C),沿着垂直于电场线方向以2×107m/s的速度飞入,则
(1)电子能否飞离平行金属板正对空间?
(2)如果由A到B分布宽1cm的电子带通过此电场,能飞离电场的电子数占总数的百分之几?
一质量为 ,带电量为+q的小球从距地面高h处以一定初速度水平抛出。在距抛出点水平距离L处,有一根管口比小球直径略大的竖直细管,管上口距地面h/2,为使小球能无碰撞地通过管子,可在管子上方的整个区域加一个场强方向水平向左的匀强电场,如图所示,求:
,带电量为+q的小球从距地面高h处以一定初速度水平抛出。在距抛出点水平距离L处,有一根管口比小球直径略大的竖直细管,管上口距地面h/2,为使小球能无碰撞地通过管子,可在管子上方的整个区域加一个场强方向水平向左的匀强电场,如图所示,求:
(1)小球初速v0;
(2)电场强度E的大小;
(3)小球落地时动能EK。
为研究静电除尘,有人设计了一个盒状容器,容器侧面是绝缘的透明有机玻璃,它的上下底面是面积 的金属板,间距
的金属板,间距 ,当连接到
,当连接到 的高压电源正负两极时,能在两金属板间产生一个匀强电场,如图所示。现把一定量均匀分布的烟尘颗粒密闭在容器内,每立方米有烟尘颗粒
的高压电源正负两极时,能在两金属板间产生一个匀强电场,如图所示。现把一定量均匀分布的烟尘颗粒密闭在容器内,每立方米有烟尘颗粒 个,假设这些颗粒都处于静止状态,每个颗粒带电量为
个,假设这些颗粒都处于静止状态,每个颗粒带电量为 ,质量为
,质量为 ,不考虑烟尘颗粒之间的相互作用和空气阻力,并忽略烟尘颗粒所受重力。求合上电键后:
,不考虑烟尘颗粒之间的相互作用和空气阻力,并忽略烟尘颗粒所受重力。求合上电键后:
(1)经过多长时间烟尘颗粒可以被全部吸附?
(2)除尘过程中电场对烟尘颗粒共做了多少功?
(3)经过多长时间容器中烟尘颗粒的总动能达到最大?