已知点P(-2,-3)和以Q为圆心的圆(x-4)2+(y-2)2=9.
(1)画出以PQ为直径,Q′为圆心的圆,再求出它的方程.
(2)作出以Q为圆心的圆和以Q′为圆心的圆的两个交点A、B.直线PA、PB是以Q为圆心的圆的切线吗?为什么?
(3)求直线AB的方程.
(本题8分)已知直线l1:2x-y+2=0与l2:x+2y-4=0,点P(1, m).
(Ⅰ)若点P到直线l1, l2的距离相等,求实数m的值;
(Ⅱ)当m=1时,已知直线l经过点P且分别与l1, l2相交于A, B两点,若P恰好
平分线段AB,求A, B两点的坐标及直线l的方程.
(本题8分)如图,已知点A(2,3), B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.
(Ⅰ)求AB边上的高CE所在直线的方程;
(Ⅱ)求△ABC的面积.
(本题6分)如图,已知圆锥的轴截面ABC是边长为2的正三角形,O是底面圆心.
(Ⅰ)求圆锥的表面积;
(Ⅱ)经过圆锥的高AO的中点O¢作平行于圆锥底面的截面,求截得的圆台的体积.
(本题6分)已知直线l的倾斜角为135°,且经过点P(1,1).
(Ⅰ)求直线l的方程;
(Ⅱ)求点A(3,4)关于直线l的对称点A¢的坐标.
(选修4-5)已知函数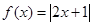 ,
, 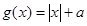
(Ⅰ)当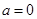 时,解不等式
时,解不等式 ;
;
(Ⅱ)若存在 ,使得
,使得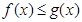 成立,求实数
成立,求实数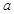 的取值范围.
的取值范围.