如图,四棱锥P—ABCD的底面是AB=2,BC= 的矩形,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD
的矩形,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD
(I)证明:侧面PAB⊥侧面PBC;
(II)求侧棱PC与底面ABCD所成的角;
(III)求直线AB与平面PCD的距离.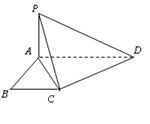
如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD= .
.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角P—CD—B的大小;
(Ⅲ)求点C到平面PBD的距离. 
在直角梯形P1DCB中,P1D//CB,CD//P1D且P1D = 6,BC = 3,DC = ,A是P1D的中点,沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°角,设E、F分别是线段AB、PD的中点.
,A是P1D的中点,沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°角,设E、F分别是线段AB、PD的中点.
(1)求证:AF//平面PEC;
(2)求平面PEC和平面PAD所成的二面角的大小;
(3)求点D到平面PEC的距离.

目前高中毕业会考中,成绩在85~100为“A”,70~84为“B”,60~69为“C”,60分以下为“D”.编制程序,输入学生的考试成绩(百分制,若有小数则四舍五入),输出相应的等级.
对某400件元件进行寿命追踪调查情况频率分布如下:
| 寿命(h) |
频率 |
| 500~600 |
0.10 |
| 600~700 |
0.15 |
| 700~800 |
0.40 |
| 800~900 |
0.20 |
| 900~1000 |
0.15 |
| 合计 |
1 |
(1)估计元件寿命在500~800 h以内的频率;
(2)估计元件寿命在800 h以上的频率.