如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD= .
.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角P—CD—B的大小;
(Ⅲ)求点C到平面PBD的距离. 
已知A、B、C是直线l上的三点,向量,,满足:
-[y+2f /(1)]+ln(x+1)=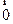 .
.
(Ⅰ)求函数y=f(x)的表达式;
(Ⅱ)若x>0,证明:f(x)>;
(Ⅲ)若不等式x2≤f(x2)+m2-2bm-3时,x∈[-1,1]及b∈[-1,1]都恒成立,求实数m的取值范围.
已知函数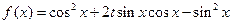 ,(1)当
,(1)当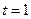 时,若
时,若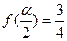 ,试求
,试求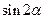 ;(2)若函数
;(2)若函数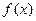 在区间
在区间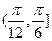 上是增函数,求实数
上是增函数,求实数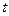 的取值范围.
的取值范围.
设关于x的一元二次方程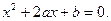 (1)若
(1)若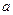 是从0,1,2,3四个数中任取一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率。(2)若
是从0,1,2,3四个数中任取一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率。(2)若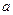 是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
在△ABC中,角A、B、C所对的边分别是a,b,c,且 (1)求
(1)求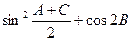 的值;(2)若b=2,求△ABC面积的最大值.
的值;(2)若b=2,求△ABC面积的最大值.
(本小题满分14分)
已知函数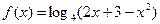 ,
,
(1)求 的定义域;
的定义域;
(2)求 的单调区间并指出其单调性;
的单调区间并指出其单调性;
(3)求 的最大值,并求取得最大值时的
的最大值,并求取得最大值时的 的值。
的值。