某寻呼台共有客户3000人,若寻呼台准备了100份小礼品,邀请客户在指定时间来领取.假设任一客户去领奖的概率为4%.问:寻呼台能否向每一位顾客都发出奖邀请?若能使每一位领奖人都得到礼品,寻呼台至少应准备多少礼品?
(本小题14分)设数列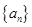 的前
的前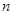 项和
项和 满足:
满足: ,等比数列
,等比数列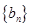 满足:
满足: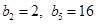
(1)求数列 的通项公式;
的通项公式;
(2)求数列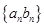 的前
的前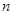 项和
项和 .
.
(本小题满分14分)如图,平面 平面
平面 ,
,
 ,
, ,
,
(1)求证: ;
;
(2)求证:
(本小题满分14分)在平面直角坐标系 中,已知
中,已知 的顶点坐标为
的顶点坐标为 .
.
(1)求直线 的方程;
的方程;
(2)求边 上高
上高 所在的直线方程.
所在的直线方程.
以数列 的任意相邻两项为坐标的点
的任意相邻两项为坐标的点 (
( )都在一次函数
)都在一次函数 的图象上,数列
的图象上,数列 满足
满足 .
.
(1)求证:数列 是等比数列;
是等比数列;
(2)设数列 ,
, 的前
的前 项和分别为
项和分别为 ,且
,且 ,求
,求 的值.
的值.
如图,直角三角形ABC的顶点坐标A( )、B(0,
)、B(0, ),顶点C在x轴上,点P为线段OA的中点,设圆M是△ABC的外接圆,若DE是圆M的任意一条直径,试探究
),顶点C在x轴上,点P为线段OA的中点,设圆M是△ABC的外接圆,若DE是圆M的任意一条直径,试探究 是否是定值?若是,求出定值;若不是,请说明理由.
是否是定值?若是,求出定值;若不是,请说明理由.