圆柱形罐的直径为10cm,高为20cm,将两个直径为8cm的铁球放于罐中,
(1)求上面铁球球心到圆柱形罐顶的距离;
(2)若向罐中注水至刚好盖过上面的铁球,求需要多少水?
已知0<β<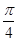 <α<
<α<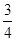 π,cos(
π,cos(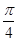 -α)=
-α)=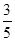 ,sin(
,sin( +β)=
+β)= ,求sin(α+β)的值.
,求sin(α+β)的值.
已知cosα=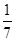 ,cos(α-β)=
,cos(α-β)=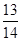 ,且0<β<α<
,且0<β<α<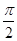 ,求β.
,求β.
求值:tan20°+tan40°+ tan20°tan40°.
tan20°tan40°.
设a= ,b=(4sinx,cosx-sinx),f(x)=a·b.
,b=(4sinx,cosx-sinx),f(x)=a·b.
(1)求函数f(x)的解析式;
(2)已知常数ω>0,若y=f(ωx)在区间 上是增函数,求ω的取值范围;
上是增函数,求ω的取值范围;
(3)设集合A= ,B={x||f(x)-m|<2},若A
,B={x||f(x)-m|<2},若A B,求实数m的取值范围.
B,求实数m的取值范围.
已知a>0,函数f(x)=-2asin +2a+b,当x∈
+2a+b,当x∈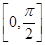 时,-5≤f(x)≤1.
时,-5≤f(x)≤1.
(1)求常数a、b的值;
(2)设g(x)=f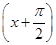 且lgg(x)>0,求g(x)的单调区间.
且lgg(x)>0,求g(x)的单调区间.