已知a>0,函数f(x)=-2asin +2a+b,当x∈
+2a+b,当x∈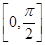 时,-5≤f(x)≤1.
时,-5≤f(x)≤1.
(1)求常数a、b的值;
(2)设g(x)=f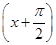 且lgg(x)>0,求g(x)的单调区间.
且lgg(x)>0,求g(x)的单调区间.
已知函数 .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)讨论函数 在区间
在区间 上零点的个数.
上零点的个数.
已知椭圆的焦点在 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线 的焦点,离心率
的焦点,离心率 ,过椭圆的右焦点
,过椭圆的右焦点 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线 交椭圆于
交椭圆于 两点.
两点.
(1)求椭圆方程;
(2)设点 是线段
是线段 上的一个动点,且
上的一个动点,且 ,求
,求 的取值范围;
的取值范围;
(3)设点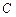 是点
是点 关于
关于 轴对称点,在
轴对称点,在 轴上是否存在一个定点
轴上是否存在一个定点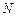 ,使得
,使得 三点共线?若存在,求出定点
三点共线?若存在,求出定点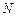 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
已知数列 的首项
的首项 ,前
,前 项和为
项和为 ,且
,且 .
.
(1)求数列 的通项;
的通项;
(2)令 ,求函数
,求函数 在
在 处的导数
处的导数 .
.
四棱锥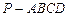 中,底面
中,底面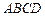 是边长为2的正方形,
是边长为2的正方形,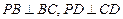 ,且
,且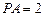 ,点
,点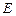 满足
满足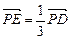 .
.
(1)求证: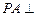 平面
平面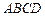 ;
;
(2)求二面角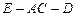 的余弦值;
的余弦值;
(3)在线段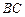 上是否存在点
上是否存在点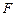 使得
使得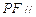 平面
平面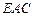 ?若存在,确定点
?若存在,确定点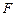 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.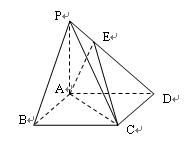
已知集合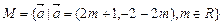 ,
,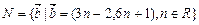 ,且
,且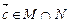 ,设函数
,设函数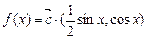 .
.
(1)求函数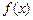 的单调减区间;
的单调减区间;
(2)当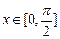 时,求
时,求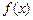 的最大值和最小值.
的最大值和最小值.