四棱锥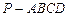 中,底面
中,底面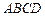 是边长为2的正方形,
是边长为2的正方形,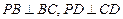 ,且
,且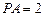 ,点
,点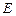 满足
满足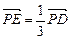 .
.
(1)求证: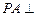 平面
平面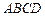 ;
;
(2)求二面角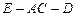 的余弦值;
的余弦值;
(3)在线段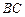 上是否存在点
上是否存在点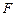 使得
使得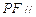 平面
平面 ?若存在,确定点
?若存在,确定点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.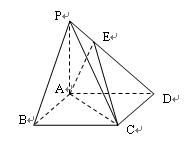
已知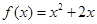 ,且有
,且有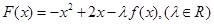 .
.
(1)若 在
在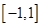 上是增函数,求实数
上是增函数,求实数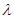 的取值范围;
的取值范围;
(2)试判断是否存在正数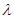 ,使函数
,使函数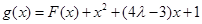 在区间
在区间 上的值域为
上的值域为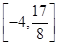 ,若存在求出
,若存在求出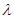 值;若不存在说明理由.
值;若不存在说明理由.
已知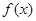 为
为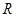 上的奇函数,
上的奇函数,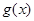 为
为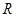 上的偶函数,且满足
上的偶函数,且满足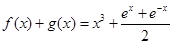 .
.
(1)求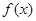 与
与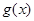 的解析式,指出
的解析式,指出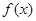 的单调性(单调性不要求证明);
的单调性(单调性不要求证明);
(2)若关于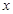 不等式
不等式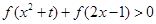 恒成立,求
恒成立,求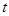 的取值范围;
的取值范围;
(3)若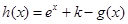 在
在 上有唯一零点,求
上有唯一零点,求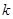 的取值范围.
的取值范围.
有一种候鸟每年都按一定的路线迁陟,飞往繁殖地产卵.科学家经过测量发现候鸟的飞行速度可以表示为函数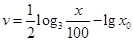 ,单位是
,单位是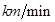 ,其中
,其中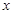 表示候鸟每分钟耗氧量的单位数,
表示候鸟每分钟耗氧量的单位数,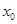 表示测量过程中候鸟每分钟的耗氧偏差.(参考数据:
表示测量过程中候鸟每分钟的耗氧偏差.(参考数据: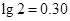 ,
,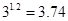 ,
,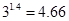 )
)
(1)若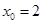 ,候鸟每分钟的耗氧量为
,候鸟每分钟的耗氧量为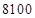 个单位时,它的飞行速度是多少
个单位时,它的飞行速度是多少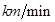 ?
?
(2)若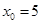 ,候鸟停下休息时,它每分钟的耗氧量为多少个单位?
,候鸟停下休息时,它每分钟的耗氧量为多少个单位?
(3)若雄鸟的飞行速度为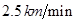 ,雌鸟的飞行速度为
,雌鸟的飞行速度为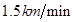 ,那么此时雄鸟每分钟的耗氧量是雌鸟每分钟的耗氧量的多少倍?
,那么此时雄鸟每分钟的耗氧量是雌鸟每分钟的耗氧量的多少倍?
已知 (
( 是常数)为幂函数,且在第一象限单调递增.
是常数)为幂函数,且在第一象限单调递增.
(1)求 的表达式;
的表达式;
(2)讨论函数 在
在 上的单调性,并证之.
上的单调性,并证之.
函数 满足
满足 .
.
(1)若 ,求
,求 的值域;
的值域;
(2)令 ,判定函数
,判定函数 的奇偶性,并证明.
的奇偶性,并证明.