如图所示,坐标系中第一象限有垂直纸面向外的匀强磁场,磁感应强度B=102T,同时有竖直向上与y轴同方向的匀强电场,场强大小E1=102V/m,第四象限有竖直向上与y轴同方向的匀强电场,场强大小E2=2E1=2×102V/m。若有一个带正电的微粒,质量m=10-12kg,电量q=10-13C,以水平与x轴同方向的初速度从坐标轴的P1点射入第四象限,OP1=0.2m,然后从x轴上的P2点穿入第一象限,OP2=0.4m,接着继续运动。取g=10m/s2。求:
(1)微粒射入的初速度;
(2)微粒第三次过x轴的位置;
(3)从P1开始到第三次过x轴的总时间。
科研人员乘气球进行科学考察.气球、座舱、压舱物和科研人员的总质量为990 kg.气球在空中停留一段时间后,发现气球漏气而下降,及时堵住.堵住时气球下降速度为1 m/s,且做匀加速运动,4 s内下降了12 m.为使气球安全着陆,向舱外缓慢抛出一定的压舱物.此后发现气球做匀减速运动,下降速度在5分钟内减少3 m/s.若空气阻力和泄漏气体的质量均可忽略,重力加速度g=9.89 m/s2,求抛掉的压舱物的质量.
“神舟”六号飞船完成了预定空间科学和技术试验任务后,返回舱于2005年10月17日4时11分开始从太空向地球表面按预定轨道返回,在离地10km的高度打开阻力降落伞减速下降,这一过程中若返回舱所受阻力与速度的平方成正比,比例系数(空气阻力系数)为k,设返回舱总质量M=3000kg,所受空气浮力恒定不变,且认为竖直降落。从某时刻开始计时,返回舱的运动v-t图象如图中的AD曲线所示,图中AB是曲线在A点的切线,切线交于横轴一点B的坐标为(8,0),CD是平行横轴的直线,交纵轴于C点C的坐标为(0,8)。g=10m/s2,请解决下列问题:
(1)在初始时刻v0=160m/s时,它的加速度多大?
(2)推证空气阻力系数k的表达式并算出其数值。
(3)返回舱在距离高度h=1m时,飞船底部的4个反推力小火箭点火工作,使其速度由8m/s迅速减至1m/s后落在地面上,若忽略燃料质量的减少对返回舱总质量的影响,并忽略此阶段速度变化而引起空气阻力的变化,试估算每支小火箭的平均推力(计算结果取两位有效数字)
如图所示,质量M=4kg的木板B静止于光滑的水平面上,其左端带有挡板,上表面长L=1m,木板右端放置一个质量m=2kg的木块A(可视为质点),A与B之间的动摩擦因素μ=0.2。现在对木板B施加一个水平向右的恒力F=14N,使B向右加速运动,经过一段时间后,木块A将与木板B左侧的挡板相碰撞,在碰撞前的瞬间撤去水平恒力F。已知该碰撞过程时间极短且无机械能损失,假设A、B间的最大静摩擦力跟滑动摩擦力相等,g取10m/s2。,试求:
(1)撤去水平恒力F的瞬间A、B两物体的速度大小vA、VB分别多大
(2)此过程F所做的功;
(3)撤去水平恒力F前因摩擦产生的热量。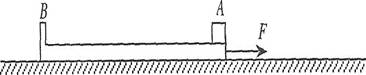
如图2-30,一个弹簧台秤的秤盘质量和弹簧质量都可以不计,盘内放一个物体P处于静止。P的质量为12kg,弹簧的劲度系数k=800N/m。现给P施加一个竖直向上的力F,使P从静止开始向上做匀加速运动。已知在前0.2s内F是变化的,在0.2s以后F是恒力,则F的最小值是多少,最大值是多少?(g=10m/s2)
如图所示,质量为M的汽车通过质量不计的绳索拖着质量为m的车厢(可作为质点)在水平地面上由静止开始做直线运动.已知汽车和车厢与水平地面间的动摩擦因数均为m,汽车和车厢之间的绳索与水平地面间的夹角为q,汽车的额定功率为P,重力加速度为g,不计空气阻力.为使汽车能尽快地加速到最大速度又能使汽车和车厢始终保持相对静止,问:
(1)汽车所能达到的最大速度为多少?
(2)汽车能达到的最大加速度为多少?
(3)汽车以最大加速度行驶的时间为多少?