如图所示,直三棱柱ABC—A1B1C1中,B1C1=A1C1,AC1⊥A1B,M、N分别是A1B1、AB的中点.
(1)求证:C1M⊥平面A1ABB1;
(2)求证:A1B⊥AM;
(3)求证:平面AMC1∥平面NB1C;
(4)求A1B与B1C所成的角.
(本小题满分12分)为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x(单位:小时)与当天投篮命中率y之间的关系:
| 时间x |
1 |
2 |
3 |
4 |
5 |
| 命中率y |
0.4 |
0.5 |
0.6 |
0.6 |
0.4 |
(1)求小李这5天的平均投篮命中率;
(2)用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率.
(本小题满分12分)已知三棱锥 中,侧棱垂直于底面,点
中,侧棱垂直于底面,点 是
是 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)若底面 为边长为
为边长为 的正三角形,
的正三角形, ,求三棱锥
,求三棱锥 的体积.
的体积.
(本小题满分12分)在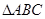 中,角
中,角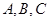 的对边分别为
的对边分别为 ,已知
,已知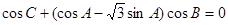 .
.
(Ⅰ)求角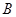 的大小;
的大小;
(Ⅱ)若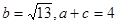 ,求△
,求△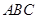 的面积.
的面积.
(本小题满分12分)设函数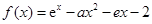 ,其中
,其中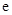 为自然对数的底数.
为自然对数的底数.
(Ⅰ) 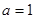 时,求曲线
时,求曲线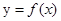 在点
在点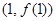 处的切线方程;
处的切线方程;
(Ⅱ)函数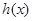 是
是 的导函数,求函数
的导函数,求函数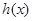 在区间
在区间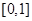 上的最小值.
上的最小值.
(本小题满分12分)已知椭圆C: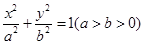 过点
过点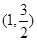 ,且椭圆C的离心率为
,且椭圆C的离心率为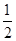 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若动点P在直线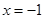 上,过P作直线交椭圆C于M,N两点,且P为线段MN中点,再过P作直线
上,过P作直线交椭圆C于M,N两点,且P为线段MN中点,再过P作直线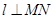 .证明:直线
.证明:直线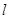 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.