如图所示，水平桌面上有两根相距为L=20cm，足够长的的水平平行光滑导轨，导轨的一端连接电阻R=0.9Ω，若在导轨平面上建立直角平面坐标系，取与导轨平行向右方向为x轴正方向，而与导轨垂直的水平方向为y轴方向。在x < 0的一侧没有磁场，在x > 0的一侧有竖直向下的磁场穿过导轨平面。该磁场磁感应强度的大小沿y轴方向均匀，但沿x轴方向随x的增大而增大，且B=kx，式中k=15/4T/m。质量为M的金属杆AB水平而与导轨垂直放置，可在导轨上沿与导轨平行的方向运动，当t=0时，AB位于x=0处，并有沿x轴正方向的初速度v0=5m/s。在运动过程中，有一大小变化的沿x轴方向的水平拉力F作用于AB，使AB有沿x轴负方向、大小为a=10m/s2的恒定加速度作匀变速直线运动。除R外，其它电阻均忽略不计。求：
（1）该回路中产生感应电流可以持续的时间；
（2）当AB向右运动的速度为3 m/s时，回路中的感应电动势的大小；
（3）若满足x < 0时F=0，求AB经1.6s时的位置坐标，并写出AB向右运动时拉力F与时间t的函数关系（直接用a、v0、M、k、R、L表示），以及在0.6s时金属杆AB受到的磁场力。
如图所示,一不透明的圆柱形容器内装满折射率为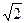
的透明液体,容器底部正中央O点处有一点光源S,平面镜MN与底面成45°角放置.若容器高为2 dm,底边半径为(1+
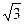) dm,OM="1" dm,在容器中央正上方1 dm处水平放置一足够长的刻度尺.求光源S发出的光线经平面镜反射后,照射到刻度尺上的长度.(不考虑容器侧壁和液面的反射)
半径为R的玻璃半圆柱体，横截面如图所示，圆心为O.一束单色红光沿截面射向圆柱面，方向与底面垂直,AO为与底面垂直的半径,光线的入射点为B，∠AOB=60°.已知该玻璃对红光的折射率n=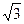
.求：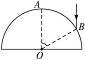
（1）光线经柱面折射后与底面的交点到O点的距离d;
（2）若入射的是单色蓝光，则距离d将比上面求得的结果大还是小.
半径为R的玻璃半圆柱体，横截面积如图4-1-7所示，圆心为O.两条平行单色红光沿截面射向圆柱面，方向与底面垂直.光线1的入射点A为圆柱的顶点，光线2的入射点为B，∠AOB=60°.已知玻璃对红光的折射率n=3.求：
图4-1-7
（1）两条光线经柱面和底面折射后的交点与O点的距离d;
（2）若入射光是单色的蓝光，则距离d将比上面求得的结果大还是小.
在地质考察中发现一个溶洞，洞内有一块立于水中的礁石,如图14-1-14所示.为了能在洞外对礁石进行观察，必须用灯光对它照明.若利用水面反射来照明，则灯应放在什么位置才有可能照亮全部礁石？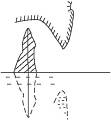
图14-1-14
如图所示,透明介质球的半径为R,光线DC平行于直径AB射到介质球的C点,DC与AB的距离H=0.8R.
(1)试证明:DC光线进入介质球后,第一次再到达介质球的界面时,在界面上不会发生全反射.(要求说明理由)
(2)若DC光线进入介质球后,第二次再到达介质球的界面时,从球内折射出的光线与
入射光线DC平行,求介质的折射率.