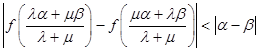在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交 作品的件数按5天一组分组统计,绘制了频率分布直方图(如图所示),已知从左到右各长方形高的比为2∶3∶4∶6∶4∶1,第三组的频数为12,请解答下列问题: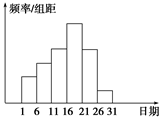
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组获奖率高?
某工厂有一批货物由海上从甲地运往乙地,已知轮船的最大航行速度为60海里/小时,甲地至乙地之间的海上航行距离为600海里,每小时的运输成本由燃料费和其它费用组成,轮船每小时的燃料费与轮船速度的平方成正比,比例系数为0.5,其它费用为每小时1250元.
(1)请把全程运输成本 (元)表示为速度
(元)表示为速度 (海里/小时)的函数,并指明定义域;
(海里/小时)的函数,并指明定义域;
(2)为使全程运输成本最小,轮船应以多大速度行驶?
已知函数 ,
,
(1)求函数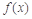 的对称轴所在直线的方程;
的对称轴所在直线的方程;
(2)求函数 单调递增区间.
单调递增区间.
已知函数 ,
,
(1)求函数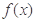 的极值;
的极值;
(2)若对 ,都有
,都有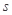 ≥
≥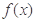 恒成立,求出
恒成立,求出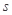 的范围;
的范围;
(3) ,有
,有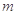 ≥
≥ 成立,求出
成立,求出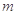 的范围;
的范围;
(1)已知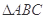 中,
中, 分别是角
分别是角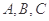 的对边,
的对边, ,则
,则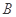 等于多少?
等于多少?
(2)在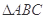 中,
中, 分别是角
分别是角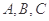 的对边,若
的对边,若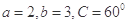 ,求边
,求边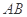 上的高
上的高 是多少?
是多少?
设关于 的方程
的方程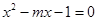 有两个实根
有两个实根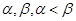 ,函数
,函数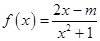 .
.
(1)求 的值;
的值;
(2)判断 在区间
在区间 的单调性,并加以证明;
的单调性,并加以证明;
(3)若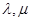 均为正实数,证明:
均为正实数,证明: