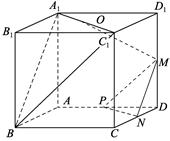
已知x1,x2,…,xn都是正数,且x1+x2+…+xn=1,求证: +
+ +…+
+…+ ≥n2.
≥n2.
已知f(x)=6co s2x-2
s2x-2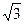 sinxcosx-3.
sinxcosx-3.
(1)求f(x)的值域及最小正周期;
(2)设锐角△ABC的内角A、B满足f (A)=2f(B)=-2
(A)=2f(B)=-2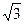 ,AB=
,AB=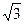 ,求B、C.
,求B、C.
已知数列 中,
中,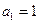 ,
,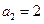 ,且
,且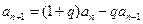
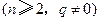 .
.
(1)设 ,证明
,证明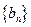 是等比数列;
是等比数列;
(2)求数列 的通项公式;
的通项公式;
(本小题满分14分)
设函数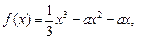
 .
.
(1) 试问函数f(x)能否在x=-1时取得极值?说明理由;
(2) 若a=-1,当x∈[-3,4]时,函数f(x)与g(x)的图像有两个公共点,求c的取值范围.
(本小题满分12分)
已知{an}是递增的等差数列,满足a2·a4=3,a1+a5="4."
(1) 求数列{an}的通项公式和前n项和公式;
(2) 设数列{bn}对n∈N*均有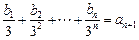 成立,求数列{bn}的通项
成立,求数列{bn}的通项 公式.
公式.
(本小题满分12分)
如图:在正方体ABCD—A1B1C1D1中,M、N、P分别为所在边的中点,O为面对角线A1C1的中点.
(1) 求证:面MNP∥面A1C1B;(2) 求证:MO⊥面A1C1.