如果在一星球上,宇航员为了估测星球的平均密度,设计了一个简单的实验:他先利用手表,记下一昼夜的时间T;然后,用弹簧秤测一个砝码的重力,发现在赤道上的重力仅为两极的90%.试写出星球平均密度的估算式.
某汽车发动机的额定功率为60 kW,在水平路面上行驶时所受的阻力是1 800 N,汽车以额定功率行驶,求:
(1)汽车行驶的最大的速度;
(2)汽车行驶的速度为15 m/s时的牵引力.
利用斜面从货车上卸货物,每包货物的质量m="20" kg,斜面的倾角α=37°,斜面的长度l="0.5" m,货物与斜面之间的动摩擦因数μ=0.2,求:
(1)货物从斜面顶端滑到底端的过程中受到的各个力所做的功;
(2)外力做的总功(g取10 m/s2).
图7-2-6所示的是一学生骑车爬坡的情形.假如他骑车时的最大功率是1 200 W,车和学生的总质量是75 kg,斜坡倾角为20°,运动过程中受到的摩擦阻力恒为60 N,则此学生骑车上坡的最大速度是多少?假如他在水平路面上骑车,最大速度可达到多少?(取g="10" m/s2)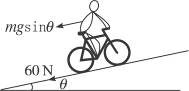
图7-2-6
汽车的质量为4×103 kg,额定功率为30 kW,运动中阻力大小恒为车重的0.1倍.汽车在水平路面上从静止开始以8×103 N的牵引力出发,求:(g取10 m/s2)
(1)经过多长时间汽车达到额定功率?
(2)汽车达到额定功率后保持功率不变,运动中最大速度是多大?
(3)汽车加速度为0.6 m/s2时速度是多大?
质量为m、发动机的额定功率为P0的汽车沿平直公路行驶,当它的加速度为a时,速度为v,测得发动机的实际功率为P1.假定运动中所受阻力恒定,它在平直公路上匀速行驶的最大速度是多少?