在地面附近的真空中，存在着竖直向上的匀强电场和垂直电场方向水平向里的匀强磁场，如图甲所示。磁场随时间变化情况如图乙所示．该区域中有一条水平直线MN，D是MN上的一点．在t=O时刻，有一个质量为m、电荷量为+q的小球(可看作质点)，从M点开始沿着水平直线以速度
做匀速直线运动，
时刻恰好到达N点．经观测发现，小球在t=2至t=3时间内的某一时刻，又竖直向下经过直线MN上的D点，并且以后小球多次水平向右或竖直向下经过D点．求：
(1)电场强度E的大小；
(2)小球从M点开始运动到第二次经过D点所用的时间；
(3)小球运动的周期，并画出运动轨迹(只画一个周期)．
甲 乙
如图所示，R为电阻箱，V为理想电压表．当电阻箱读数为R1=2Ω时，电压表读数为U1=4V；当电阻箱读数为R2=5Ω时，电压表读数为U2=5V．求：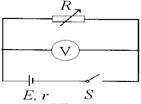
(1)电源的电动势E和内阻r.
(2)当电阻箱R读数为多少时，电源的输出功率最大?最大值Pm为多少?
如图所示是说明示波器工作原理的示意图，已知两平行板间的距离为d、板长为l 。 电子经电压为U1的电场加速后从两平行板间的中央处垂直进入偏转电场，设电子质量为m、电量为e 。求：
（1）经电场加速后电子速度v的大小；
（2）要使电子离开偏转电场时的偏转角度最大，
两平行板间的电压U2应是多大？
如图所示，水平放置的平行板电容器，两板间距为d=8cm，板长为L=25cm，接在直流电源上，有一带电液滴以v0=0.5m/s的初速度从板间的正中点水平射入，恰好做匀速直线运动，当它运动到P处时迅速将下板向上提起4/3cm，液滴刚好从金属板末端飞出，求：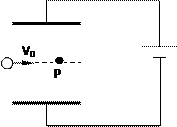
（1）下极板上提后液滴经过P点以后的加速度（g取10m/s2）
（2）液滴从射入开始匀速运动到P点所用时间。
如图所示，E="10" V，r="1" Ω，R1=R3="5" Ω，R2="4" Ω，C="100" μF. S断开.求：当S闭合后流过R3的总电荷量.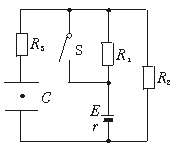
如图7所示，在匀强电场中，一质量为m，带电量q的小球（看成质点）被长为L的细线吊起，当球静止时，细线与竖直方向的夹角为θ，则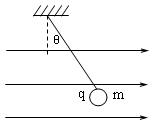
(1).判断小球带电的电性。
(2).计算电场场强的大小。