如图所示,半径分别为R和r (R>r)的甲乙两光滑圆轨道安置在同一竖直平面内,两轨道之间由一条光滑水平轨道CD相连,在水平轨道CD上一轻弹簧a、b被两小球夹住,同时释放两小球,a、b球恰好能通过各自的圆轨道的最高点,求:
(1)两小球的质量比.
(2)若ma=mb=m,要求ab都能通过各自的最高点,弹簧释放前至少具有多少弹性势能.
的距离。
A、B两站相距s,将其分成n段,汽车无初速由A站出发,分n段向B站做匀加速直线运动,第一段的加速度为a.当汽车到达每一等份的末端时,其加速度增加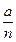 ,求汽车到达B站时的速度.[8]
,求汽车到达B站时的速度.[8]
一电梯,启动时匀加速上升,加速度为2m/s2,制动时匀减速上升,加速度为-1m/s2,楼高52m.求:
⑴若上升的最大速度为6m/s,电梯升到楼顶的最短时间是多少?
⑵如果电梯先加速上升,然后匀速上升,最后减速上升,全程共用时间为16s.上升的最大速度是多少?[8]
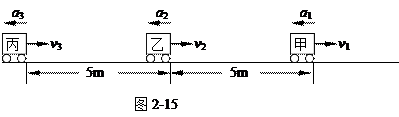
甲、乙、丙三辆车行驶在平直公路上,车速分别为6m/s、8 m/s、9 m/s.当甲、乙、丙三车依次相距5m时,乙车驾驶员发现甲车开始以1m/s2的加速度做减速运动,于是乙也立即做减速运动,丙车驾驶员也同样处理.如图2-15(原图2-23)所示.直到三车都停下来时均未发生撞车事故.求丙车减速运动的加速度至少应为多大?[8]
 |
摩托车以速度v1沿平直公路行驶,突然驾驶员发现正前方离摩托车s处,有一辆汽车正以v2的速度开始减速,且v2<v1,汽车的加速度大小为a2.为了避免发生碰撞,摩托车也同时减速,求其加速度至少需要多少?[5]
物体在斜面顶端由静止匀加速下滑,最初4s内经过路程为s1,最后4s内经过的路程s2,且s2-s1=8m,s1∶s2=1∶2,求斜面的全长.[6]