(1)如图3-3,某人投标投中圆的概率是多少(投在正方形外面或边缘不算)?
(2)同(1)中图形,利用随机模拟的方法近似计算正方形内切圆的面积,并估计π的近似值.
图3-3
(本小题12分)如图,已知直角梯形 中,
中, 且
且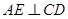 ,又
,又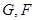 分别为
分别为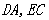 的中点,将△
的中点,将△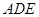 沿
沿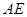 折叠,使得
折叠,使得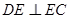 .
.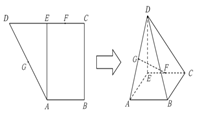
(Ⅰ)求证: ;
;
(Ⅱ)求证: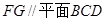 ;
;
(Ⅲ)在线段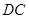 上找一点
上找一点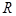 ,使得
,使得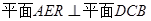 ,并说明理由.
,并说明理由.
(本小题12分)已知平行四边形 的三个顶点的坐标为
的三个顶点的坐标为 ,
, ,
,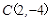 .
.
(Ⅰ)在 ABC中,求边AC中线所在直线方程;
ABC中,求边AC中线所在直线方程;
(Ⅱ)求的顶点 的坐标及对角线
的坐标及对角线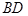 的长度;
的长度;
(Ⅲ)求平行四边形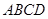 的面积及边AD所在的直线方程.
的面积及边AD所在的直线方程.
(本小题10分)如图,在四棱锥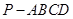 中,
中, 底面
底面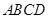 ,底面
,底面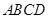 是正方形,
是正方形,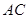 与
与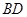 交于点
交于点 ,
,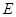 为
为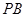 的中点.
的中点.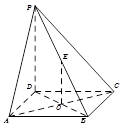
(Ⅰ)求证: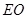 ∥平面
∥平面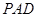 ;
;
(Ⅱ)求证:
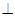
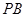 .
.
如图,正方体 的棱长为1,线段
的棱长为1,线段 上有两个动点E,F,且
上有两个动点E,F,且 ,则下列结论中错误的是()
,则下列结论中错误的是()
A. |
B.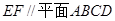 |
C.三棱锥 的体积为定值 的体积为定值 |
D. 的面积与 的面积与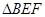 的面积相等 的面积相等 |
(本小题10分)已知圆C:x2+(y-3)2=4,一动直线l过A(-1,0)与圆C相交于P,Q两点,M是PQ的中点,l与直线m:x+3y+6=0相交于点N.
(Ⅰ)求证:当l与m垂直时,l经过圆心C;
(Ⅱ)当 =2
=2 时,求直线l的方程;
时,求直线l的方程;
(Ⅲ)请问: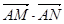 是否与直线l的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
是否与直线l的倾斜角有关,若无关,请求出其值;若有关,请说明理由.