设函数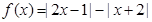
(1)求不等式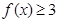 的解集;
的解集;
(2)若关于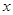 的不等式
的不等式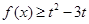 在
在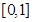 上无解,求实数
上无解,求实数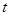 的取值范围
的取值范围
已知在直角坐标系xOy中,曲线C的参数方程为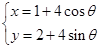 (
(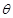 为参数),直线
为参数),直线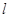 经过定点P(3,5),倾斜角为
经过定点P(3,5),倾斜角为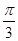 (1)写出直线
(1)写出直线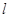 的参数方程和曲线C的标准方程;(2)设直线
的参数方程和曲线C的标准方程;(2)设直线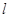 与曲线C相交于A、B两点,求
与曲线C相交于A、B两点,求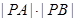 的值
的值
如图,PA、PB是圆O的两条切线,A、B是切点,C是劣弧AB(不包括端点)上一点,直线PC交圆O于另一点D,Q在弦CD上,且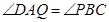 求证:
求证: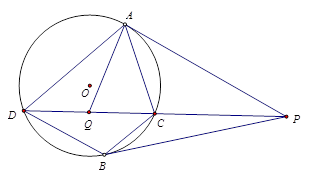
(1)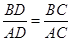 ;(2)
;(2)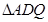 ∽
∽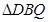
已知函数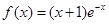 (e为自然对数的底数)
(e为自然对数的底数)
(1)求函数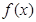 的单调区间;
的单调区间;
(2)设函数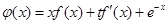 ,存在实数
,存在实数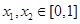 ,使得
,使得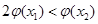 成立,求实数
成立,求实数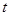 的取值范围
的取值范围
椭圆 的离心率为
的离心率为 ,且过点
,且过点 直线
直线 与椭圆M交于A、C两点,直线
与椭圆M交于A、C两点,直线 与椭圆M交于B、D两点,四边形ABCD是平行四边形
与椭圆M交于B、D两点,四边形ABCD是平行四边形
(1)求椭圆M的方程;
(2)求证:平行四边形ABCD的对角线AC和BD相交于原点O;
(3)若平行四边形ABCD为菱形,求菱形ABCD的面积的最小值