如图6-8-25甲所示,在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球,圆锥体固定在水平面上不动,其轴线沿竖直方向,母线与轴线之间的夹角为300,物体以速率v绕圆锥体轴线做水平圆周运动:
⑴当 时,求线对物体的拉力;
时,求线对物体的拉力;
⑵当 时,求线对物体的拉力。
时,求线对物体的拉力。
如图7-7-6所示,一粗细均匀的U形管内装有同种液体且竖直放置,右管口用盖板A密封一部分气体,左管开口,两液面高度差为h,U形管中液柱总长为4h.现拿去盖板,液柱开始流动,不计水的粘滞阻力,当两侧管内液面恰好相齐时,右侧液面下降的速度大小为________.
图7-7-6
如图7-7-11所示,两个物体用轻绳经光滑的滑轮拴在一起,质量分别为m1、m2,m2在地面上,m1离地的高度为h,m1>m2,由静止释放.则m1落地后,m2还能上升的高度为多少?
图7-7-11
如图7-7-10所示,质量分别为m和2m的两个小物体可视为质点,用轻质细线连接,跨过光滑圆柱体,轻的着地,重的恰好与圆心一样高.若无初速度地释放,则物体m上升的最大高度为多少?
图7-7-10
如图7-7-14所示,质量均为m的小球A、B、C,用长为l的细线相连,置于高为h的光滑水平桌面上,l>h,A球刚跨过桌边,若A球、B球相继下落着地后不再反跳,则C球离开桌边时速度的大小是多少?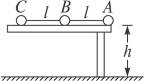
图7-7-14
如图7-7-13连接而成,列车从斜轨高处无动力静止滑下,经过圆轨道后再冲上另一斜轨.已知列车质量为m,圆轨道半径为R.若将列车看成质点,并且不计摩擦,求:
(1)要保证列车能安全通过圆轨道,则斜轨高度至少多大;
(2)若列车较长,不能看成质点,并且要考虑列车与轨道间的摩擦,则对斜轨高度有何影响.
(3)若列车由许多节构成,总长恰为2πR,列车高度不计,摩擦阻力也不考虑,为保证列车能安全通过圆轨道,求斜轨高度至少多大.
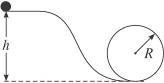
图7-7-13