某商品的市场需求量y1(万件)、市场供应量y2(万件)与市场价格x(元/件)分别近似地满足下列关系:y1=-x+70,y2=2x-20.当y1=y2时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量.
(1)求平衡价格和平衡需求量;
(2)若要使平衡需求量增加4万件,政府对每件商品应给予多少元补贴?
某商场组织有奖竞猜活动,参与者需要先后回答两道选择题,问题A有三个选项,问题B有四个选项,但都只有一个选项是正确的,正确回答问题A可获奖金25元,正确回答问题B可获奖金30元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者猜奖活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生,只能用蒙猜的办法答题.
(1)如果参与者先回答问题A,求其获得奖金25元的概率;
(2)试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大.
如图,在直三棱柱 中,
中, 平面
平面 ,其垂足
,其垂足 落在直线
落在直线 上.
上.
(1)求证: ⊥
⊥
(2)若 ,
, ,
, 为
为 的中点,求二面角
的中点,求二面角 的平面角的余弦值
的平面角的余弦值
在三角形 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且三角形的面积为
,且三角形的面积为 .
.
(1)求角 的大小
的大小
(2)若 ,求
,求 的值.
的值.
已知递增等比数列 的前n项和为
的前n项和为 ,
, ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,且
,且 的前
的前 项和
项和 .
.
求证:
已知函数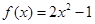 .
.
(1)用定义证明 是偶函数;
是偶函数;
(2)用定义证明 在
在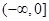 上是减函数;
上是减函数;
(3)作出函数 的图像,并写出函数
的图像,并写出函数 当
当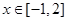 时的最大值与最小值.
时的最大值与最小值.