从高一学生中抽取50名同学参加数学竞赛,成绩的分组及各组的频数如下:(单位:分)
[40,50),2; [50,60),3; [60,70),10; [70,80),15; [80,90),12; [90,100),8.
(1)列出样本的频率分布表;
(2)画出频率分布直方图;
(3)估计成绩在[60,90)分的学生比例;
(4)估计成绩在85分以下的学生比例.
两台机床同时生产直径为10的零件,为了检验产品质量,质量质检员从两台机床的产品中各抽取4件进行测量,结果如下:
| 机床甲 |
10 |
9.8 |
10 |
10.2 |
| 机床乙 |
10.1 |
10 |
9.9 |
10 |
如果你是质量检测员,在收集到上述数据后,你将通过怎样的运算来判断哪台机床生产的零件质量更符合要求.
已知函数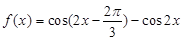 (
(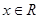 ).
).
(1)求函数 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2) 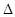
 内角
内角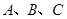 的对边长分别为
的对边长分别为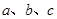 ,若
,若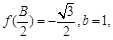
 且
且 试求角B和角C.
试求角B和角C.
等差数列 的前
的前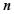 项和记为
项和记为 ,已知
,已知 ;
;
(1)求数列 的通项
的通项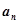
(2)若 ,求
,求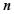
(3)令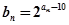 ,求数列
,求数列 的前
的前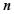 项和
项和
已知直线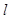 过点
过点 与圆
与圆 相切,
相切,
(1)求该圆的圆心坐标及半径长
(2)求直线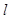 的方程
的方程