a为何值时,圆C1:x2+y2-2ax+4y+(a2-5)=0和圆C2:x2+y2+2x-2ay+(a2-3)=0有四条公切线?
(本小题满分12分)
甲乙两个班级进行一门课程的考试,按照学生考试成绩优秀和不优秀统计成绩后,得到如下的列联表:
班级与成绩列联表
| 优 秀 |
不优秀 |
|
| 甲 班 |
10 |
35 |
| 乙 班 |
7 |
38 |
根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下认为成绩与班级有关系?
附:
 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
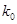 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(本小题满分10分)
求圆心为C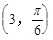 ,半径为3的圆的极坐标方程。
,半径为3的圆的极坐标方程。
(本小题满分12分)
观察以下各等式: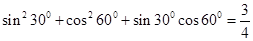

 ,
,
分析上述各式的共同特点,猜想出反映一般规律的等式,并对等式的正确性作出证明.
(本小题满分12分)
为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间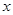 (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率 之间的关系:
之间的关系:
时间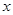 |
1 |
2 |
3 |
4 |
5 |
命中率 |
0.4 |
0.5 |
0.6 |
0.6 |
0.4 |
求小李这5天的平均投篮命中率;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率.
附:线性回归方程 中系数计算公式
中系数计算公式 ,
, ,
,
.已知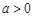 ,函数
,函数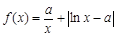 ,
,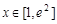 .
.
(Ⅰ)当 时,求曲线
时,求曲线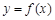 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若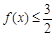 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.