在海岸A处,发现北偏东45°方向,距离A( -1)n mile的B处有一艘走私船,在A处北偏西75°的方向,距离A 2 n mile的C处的缉私船奉命以10
-1)n mile的B处有一艘走私船,在A处北偏西75°的方向,距离A 2 n mile的C处的缉私船奉命以10 n mile/h的速度追截走私船.此时,走私船正以10 n mile/h的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?
n mile/h的速度追截走私船.此时,走私船正以10 n mile/h的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?
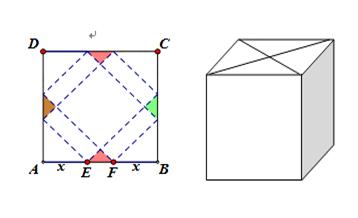
请你设计一个包装盒,如图所示,四边形ABCD是边长为60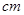 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合与图中的点P,正好形成一个正四棱柱形状的包装盒。E,F在AB上,是被切去的一个等腰直角三角形斜边的两个端点,设
的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合与图中的点P,正好形成一个正四棱柱形状的包装盒。E,F在AB上,是被切去的一个等腰直角三角形斜边的两个端点,设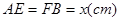 。
。
(1)某广告商要求包装盒的侧面积S 最大,试问
最大,试问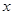 应取何值?
应取何值?
(2)某厂商要求包装盒的容积V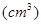 最大,试问
最大,试问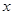 应取何值?并求出此时包装盒的高与底面边长的比值。
应取何值?并求出此时包装盒的高与底面边长的比值。
已知双曲线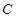 的焦点为
的焦点为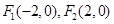 ,且离心率为2;
,且离心率为2;
(Ⅰ)求双曲线的标准方程;(Ⅱ)若经过点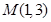 的直线
的直线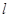 交双曲线
交双曲线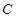 于
于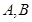 两点,且
两点,且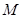 为线段
为线段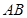 的中点,求直线
的中点,求直线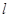 的方程。
的方程。
. (本题满分13分)
已知函数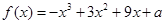
(1)求 的单调递减区间;
的单调递减区间;
(2)若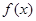 在区间
在区间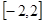 上的最大值为20,求它在该区间上的最小值。
上的最大值为20,求它在该区间上的最小值。
、(本题15分)已知函数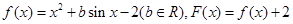 ,且对于任意实数
,且对于任意实数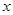 ,恒有F(x)=F(-x)。(1)求函数
,恒有F(x)=F(-x)。(1)求函数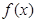 的解析式;
的解析式;
(2)已知函数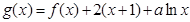 在区间
在区间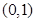 上单调,求实数
上单调,求实数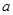 的取值范围;
的取值范围;
(3)函数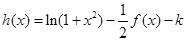 有几个零点?
有几个零点?
(本小题满分15分)已知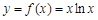 .
.
(1)求函数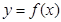 的图像在
的图像在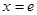 处的切线方程;
处的切线方程;
(2)设实数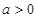 ,求函数
,求函数 在
在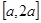 上的最大值;
上的最大值;
(3)证明对一切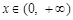 ,都有
,都有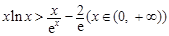 成立。
成立。