求下列函数的值域：
（1）y=
;
(2)y=sinx+cosx+sinxcosx;
(3)y=2cos
+2cosx.
已知函数f(x)＝2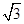
sin(2ωx＋φ)(ω＞0，φ∈(0，π))的图象中相邻两条对称轴间的距离为
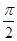，且点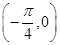
是它的一个对称中心．
(1)求f(x)的表达式；
(2)若f(ax)(a＞0)在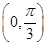
上是单调递减函数，求a的最大值．
已知函数f(x)＝2sin xcos x＋2
cos2x－，x∈R.
(1)求函数f(x)的最小正周期；
(2)在锐角△ABC中，若f(A)＝1，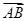
·
＝
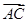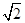，求△ABC的面积．
设函数f(x)＝
＋2cos2x.
(1)求f(x)的最大值，并写出使f(x)取最大值时x的集合；
(2)已知△ABC中，角A，B，C的对边分别为a，b，c，若f(B＋C)＝
，b＋c＝2，求a的最小值．
已知函数f(x)＝2cos2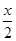
－
sin x.
(1)求函数f(x)的最小正周期和值域；
(2)若α为第二象限角，且f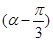
＝
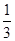，求
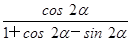的值．
在△ABC中，角A，B，C的对边分别为a，b，c，若acos2
＋ccos2
＝
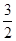b.
(1)求证：a，b，c成等差数列；
(2)若∠B＝60°，b＝4，求△ABC的面积．