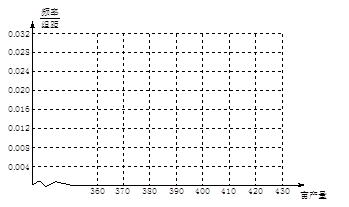某造船公司年造船量是20艘,已知造船x艘的产值函数为R(x)="3" 700x+45x2-10x3(单位:万元),成本函数为C(x)="460x+5" 000(单位:万元),又在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x).
(1)求利润函数P(x)及边际利润函数MP(x);(提示:利润=产值-成本)
(2)问年造船量安排多少艘时,可使公司造船的年利润最大?
(3)求边际利润函数MP(x)的单调递减区间,并说明单调递减在本题中的实际意义是什么?
已知 、
、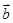 、
、 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 .
.
(1)若 ,且
,且 //
// ,求
,求 的坐标;
的坐标;
(2)若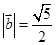 ,且
,且 与
与 垂直,求
垂直,求 与
与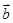 的夹角
的夹角 .
.
已知二次函数 =
=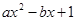 ,
, ,
, .若
.若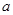 是从集合A中随机取的一个实数,
是从集合A中随机取的一个实数,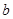 是从集合B中随机取的一个实数,求关于
是从集合B中随机取的一个实数,求关于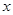 的方程
的方程 =0一根在区间
=0一根在区间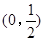 内,另一根在
内,另一根在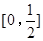 外的概率.
外的概率.
已知 的顶点坐标为
的顶点坐标为 ,
, ,
, , 点P的横坐标为14,且
, 点P的横坐标为14,且 ,点
,点 是边
是边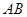 上一点,且
上一点,且 .
.
(1)求实数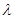 的值与点
的值与点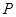 的坐标;
的坐标;
(2)求点 的坐标;
的坐标;
(3)若 为线段
为线段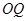 (含端点)上的一个动点,试求
(含端点)上的一个动点,试求 的取值范围.
的取值范围.
已知函数 的部分图象如图所示:
的部分图象如图所示:
(1)求 ,
,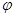 的值;
的值;
(2)设函数 ,当
,当 时,求函数
时,求函数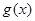 的值域.
的值域.
某良种培育基地正在培育一种小麦新品种A,种植了25亩,所得亩产数据(单位:千克)如下:
363,371,374,383,385,386,391,392,394,394,395,397,397,400,401,401,403,406,407,410,412,415,416,422,430.
(1)求这二十五个数据的中位数;
(2)以组距为10进行分组,完成答题卡上的品种A亩产量的频率分布表;
| 分组 |
频数 |
频率 |
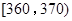 |
||
 |
||
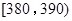 |
||
 |
||
 |
||
 |
||
| [420,430] |
||
| 合计 |
完成答题卡上的品种A亩产量的频率分布直方图.