(1)设x<y<0,试比较(x2+y2)(x-y)与(x2-y2)(x+y)的大小;
(2)已知a,b,c∈{正实数},且a2+b2=c2,当n∈N,n>2时比较cn与an+bn的大小.
(本小题满分14分)
设数列 满足
满足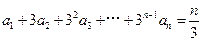 ,
, .
.
(Ⅰ)求数列 的通项;
的通项;
(Ⅱ)设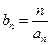 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)
从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件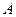 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率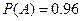 .
.
(1)求从该批产品中任取1件是二等品的概率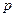 ;
;
(2)若该批产品共100件,从中任意抽取2件,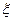 表示取出的2件产品中二等品的件数,求
表示取出的2件产品中二等品的件数,求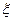 的分布列.
的分布列.
(本小题满分12分)已知函数 .
.
(Ⅰ)求函数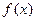 的最小正周期;
的最小正周期;
(Ⅱ)求函数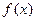 在区间
在区间 上的最小值和最大值.
上的最小值和最大值.
(本小题满分14分)
已知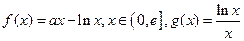 ,其中
,其中 是自然对数的底,
是自然对数的底,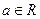

(1) 时,求
时,求 的单调区间、极值;
的单调区间、极值;
(2)是否存在实数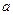 ,使
,使 的最小值是3,若存在,求出
的最小值是3,若存在,求出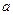 的值,若不存在,说明理由;
的值,若不存在,说明理由;
(3)在(1)的条件下,求证:

(本小题满分12分)已知数列{an}中,a1=2,前n项和为Sn,对于任意n≥2,
3Sn-4,an, 总成等差数列.
总成等差数列.
(I)求数列 通项公式an;
通项公式an;
(II)若数列 满足
满足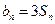 ,求数列
,求数列 的前n项和
的前n项和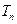 .
.