已知等差数列{an}的前n项和Sn,且对于任意的正整数n满足
=an+1.
(1)求数列{an}的通项公式;
(2)设bn=
,求数列{bn}的前n项和Bn.
【改编题】在锐角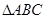
中，
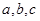分别为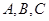
的对边,已知
．
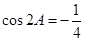（1）求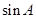
；
（2）当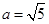
，求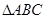的面积得最大值．
【原创】若数列
的前
项和
，则（）是等比数列 B．是等差数列
C．当
时，是等比数列 D．当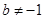
时，是等比数列
（本小题满分14分）已知函数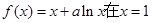
处的切线l与直线
垂直，函数
（Ⅰ）求实数
的值；
（Ⅱ）若函数
存在单调递减区间，求实数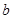
的取值范围；
（Ⅲ）设
是函数的两个极值点，若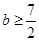
，求
的最小值．
【改编题】如图，过顶点在原点，对称轴为
轴的抛物线
上的定点
作斜率分别为
的直线，分别交抛物线于
两点．
求抛物线的标准方程和准线方程；
若
，证明：直线
恒过定点．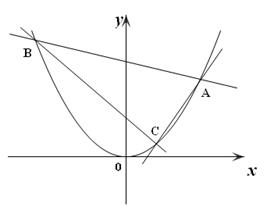
（本小题满分12分）如图，过四棱柱
形木块上底面内的一点
和下底面的对角线
将木块锯开，得到截面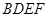
．
（1）请在木块的上表面作出过的锯线
，并说明理由；
（2）若该四棱柱的底面为菱形，四边形时矩形
，试证明：平面
平面
．