在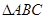 中,角
中,角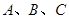 的对边分别为
的对边分别为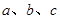 ,且
,且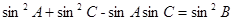 .
.
①求角 的大小;
的大小;
②求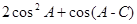 的取值范围.
的取值范围.
已知椭圆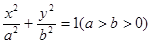 的右焦点为
的右焦点为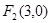 ,离心率为
,离心率为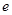 .
.
(1)若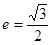 ,求椭圆的方程; (2)设直线
,求椭圆的方程; (2)设直线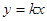 与椭圆相交于
与椭圆相交于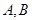 两点,
两点,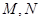 分别为线段
分别为线段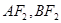 的中点.若坐标原点
的中点.若坐标原点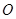 在以
在以 为直径的圆上,且
为直径的圆上,且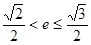 ,求
,求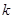 的取值范围.
的取值范围.
已知抛物线C: ,
,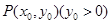 为抛物线上一点,
为抛物线上一点, 为
为 关于
关于 轴对称的点,
轴对称的点, 为坐标原点.(1)若
为坐标原点.(1)若 ,求
,求 点的坐标;
点的坐标;
(2)若过满足(1)中的点 作直线
作直线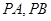 交抛物线
交抛物线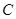 于
于 两点, 且斜率分别为
两点, 且斜率分别为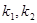 ,且
,且 ,求证:直线
,求证:直线 过定点,并求出该定点坐标.
过定点,并求出该定点坐标.
双曲线 的离心率为2,坐标原点到直线AB的距离为
的离心率为2,坐标原点到直线AB的距离为 ,其中A
,其中A ,B
,B .
.
(1)求双曲线的方程;
(2)若B1是双曲线虚轴在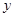 轴正半轴上的端点,过B1作直线与双曲线交于
轴正半轴上的端点,过B1作直线与双曲线交于 两点,求
两点,求 时,直线
时,直线 的方程.
的方程.
已知椭圆 的离心率
的离心率 ,A,B分别为椭圆的长轴和短轴的端点,M为AB的中点,O为坐标原点,且
,A,B分别为椭圆的长轴和短轴的端点,M为AB的中点,O为坐标原点,且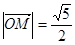 .
.
(1)求椭圆的方程;
(2)过(-1,0)的直线 交椭圆于P,Q两点,求△POQ面积最大时直线
交椭圆于P,Q两点,求△POQ面积最大时直线 的方程.
的方程.