已知函数f(x)= (ax-a-x) (a>0,且a≠1).
(ax-a-x) (a>0,且a≠1).
(1)判断f(x)的单调性;
(2)验证性质f(-x)=-f(x),当x∈(-1,1)时,并应用该性质求满足f(1-m)+f(1-m2)<0的实数m的范围.
设函数 ,且
,且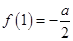 ,
,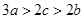 ,求证:(1)
,求证:(1) 且
且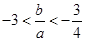 ;
;
(2)函数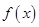 在区间
在区间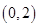 内至少有一个零点;
内至少有一个零点;
(3)设 是函数
是函数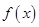 的两个零点,则
的两个零点,则 .
.
某化工企业2012年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.设该企业使用该设备 年的年平均污水处理费用为
年的年平均污水处理费用为 (万元)。
(万元)。
(1)用 表示
表示 ;
;
(2)当该企业的年平均污水处理费用最低时,企业需重新更换新的污水处理设备.则该企业几年后需要重新更换新的污水处理设备。
如图,在四棱锥 中,底面
中,底面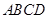 为平行四边形,
为平行四边形, ,
, ,
,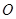 为
为 中点,
中点,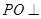 平面
平面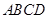 ,
,  ,
,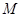 为
为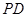 中点.
中点.
(1)证明: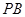 //平面
//平面 ;
;
(2)证明: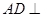 平面
平面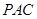 ;
;
(3)求直线 与平面
与平面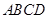 所成角的正切值.
所成角的正切值.
已知向量
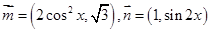 ,函数
,函数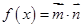
(1)求函数 的单调增区间;
的单调增区间;
(2)在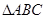 中,
中, 分别是角A, B, C的对边,且
分别是角A, B, C的对边,且 ,且
,且
求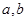 的值.
的值.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段: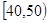 ,
,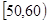 ,…,
,…,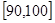 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.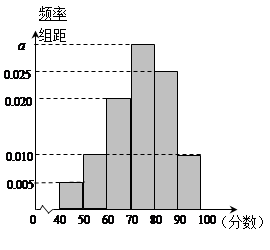
(1)求图中实数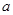 的值;
的值;
(2)若该校高一年级共有学生640人,试估计该校高一年级
期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在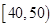 与
与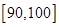 两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.