已知f(x)=logax(a>0且a≠1),设f(a1),f(a2),…,f(an) (n∈N*)是首项为4,公差为2的等差数列.
(1)设a为常数,求证:{an}成等比数列;
(2)若bn=anf(an),{bn}的前n项和是Sn,当a= 时,求Sn.
时,求Sn.
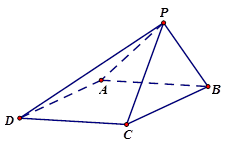
如图,已知四棱锥 的底面为菱形,
的底面为菱形, ,
,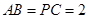 ,
,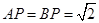 .
.
(1)求证: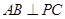 ;
;
(2)求二面角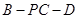 的余弦值.
的余弦值.
一个盒子里装有三张卡片,分别标记有数字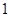 ,
, ,
,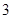 ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取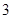 次,每次抽取
次,每次抽取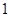 张,将抽取的卡片上的数字依次记为
张,将抽取的卡片上的数字依次记为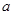 ,
,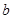 ,
,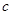 .
.
(1)求“抽取的卡片上的数字满足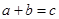 ”的概率;
”的概率;
(2)求“抽取的卡片上的数字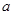 ,
,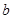 ,
,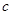 不完全相同”的概率.
不完全相同”的概率.
已知空间中三点A(-2,0,2),B(-1,1,2),C(-3,0,4),设a= ,b=
,b=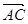 .
.
(1)求向量a与向量b的夹角的余弦值;
(2)若ka+b与ka-2b互相垂直,求实数k的值
设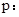 函数
函数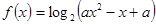 的值域为
的值域为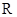 ,
,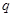 :
: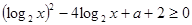 对
对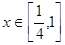 恒成立,若
恒成立,若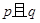 为假,
为假,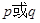 为真,求实数
为真,求实数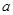 的取值范围。
的取值范围。
已知函数 (
( ).
).
(1)求函数 的单调区间;
的单调区间;
(2)函数 在定义域内存在零点,求
在定义域内存在零点,求 的取值范围.
的取值范围.
(3)若 ,当
,当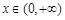 时,不等式
时,不等式 恒成立,求
恒成立,求 的取值范围
的取值范围