已知Sn是数列{an}的前n项和,且an=Sn-1+2(n≥2),a1=2.
(1)求数列{an}的通项公式;
(2)设bn= ,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得对于任意的正整数n,有Tn>
,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得对于任意的正整数n,有Tn> 恒成立?若存在,求出k的值;若不存在,说明理由.
恒成立?若存在,求出k的值;若不存在,说明理由.
如图,在四棱锥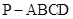 中,底面
中,底面 为直角梯形,
为直角梯形, ,
, ,平面
,平面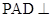 底面
底面 ,
,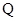 为
为 的中点,
的中点,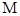 是棱
是棱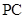 上的点,
上的点,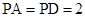 ,
,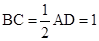 ,
, .
.
(1)求证:平面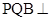 平面
平面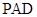 ;
;
(2)若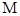 为棱
为棱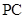 的中点,求异面直线
的中点,求异面直线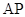 与
与 所成角的余弦值;
所成角的余弦值;
(3)若二面角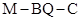 大小为
大小为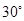 ,求
,求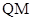 的长.
的长.
在一个盒子中,放有大小相同的红、白、黄三个小球,从中任意摸出一球,若是红球记 分,白球记
分,白球记 分,黄球记
分,黄球记 分.现从这个盒子中,有放回地先后摸出两球,所得分数分别记为
分.现从这个盒子中,有放回地先后摸出两球,所得分数分别记为 ,
, ,设
,设 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,记
,记 .
.
(1)求随机变量 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率;
取得最大值”的概率;
(2)求随机变量 的分布列和数学期望.
的分布列和数学期望.
 中,角
中,角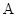 、
、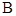 、
、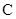 所对的边为
所对的边为 、
、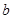 、
、 ,且
,且 .
.
(1)求角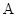 ;
;
(2)若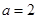 ,求
,求 的周长的最大值.
的周长的最大值.
【选修4-5:不等式选讲】
已知函数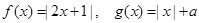
(1)当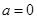 时,解不等式
时,解不等式 ;
;
(2)若存在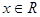 ,使得
,使得 成立,求实数
成立,求实数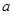 的取值范围.
的取值范围.
【选修4-4:坐标系与参数方程选讲】
已知曲线C1的参数方程是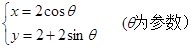 ,以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程是
,以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程是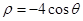 .
.
求曲线C1与C2交点的极坐标;
A、B两点分别在曲线C1与C2上,当|AB|最大时,求 的面积(O为坐标原点)
的面积(O为坐标原点)