(本小题满分15分)已知等差数列{an}中,首项a1=1,公差d为整数,且满足a1+3<a3,a2+5>a4,数列{bn}满足 ,其前n项和为Sn.(1)求数列{an}的通项公式an;(2)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.
,其前n项和为Sn.(1)求数列{an}的通项公式an;(2)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.
(本小题满分16分)设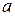 为实数,函数
为实数,函数 .(1)若
.(1)若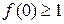 ,求
,求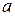 的取值范围;(2)求
的取值范围;(2)求 的最小值;(3)设函数
的最小值;(3)设函数 ,求不等式
,求不等式 的解集.
的解集.
(本小题满分16分)某连锁分店销售某种商品,每件商品的成本为4元,并且每件商品需向总店交a元(1≤a≤3)的管理费,预计当每件商品的售价为 元(8≤x≤9)时,一年的销售量为(10-x)2万件.(1)求该连锁分店一年的利润L(万元)与每件商品的售价x的函数关系式L(x);
元(8≤x≤9)时,一年的销售量为(10-x)2万件.(1)求该连锁分店一年的利润L(万元)与每件商品的售价x的函数关系式L(x);
(2)当每件商品的售价为多少元时,该连锁分店一年的利润L最大,并求出L的最大值M(a).
正三棱柱ABC—A1B1C1的底面边长为a,侧棱长为 a.
a.
(1)建立适当的坐标系,并写出A、B、A1、C1的坐标;
(2)求AC1与侧面ABB1A1所成的角.
设α,β是方程x2-ax+b=0的两个实根,试分析a>2且b>1是两根α、β均大于1的什么条件?