一矩形线圈,在匀强磁场中绕垂直磁感线的对称轴转动,形成如下图所示的交变电动势图象,试根据图象求:
(1)线圈转动的角速度;
(2)电动势的有效值;
(3)t = 1.0×10−2s时,线圈平面和磁场方向的夹角。
如图所示电路中,当滑动变阻器的滑片P向左移动时,各表(各电表内阻对电路的影响均不考虑)的示数如何变化?为什么?
用伏安法测一节干电池的电动势和内电阻,伏安图象如图所示,根据图线回答:
(1)干电池的电动势和内电阻各多大?
(2)图中a点对应的外电路电阻是多大?电源此时内部热功率是多少?
(3)图中a、b两点对应的外电路电阻之比是多大?对应的输出功率之比是多大?
(4)在此实验中,电源最大输出功率是多大?
正电子发射计算机断层(PET)是分子水平上的人体功能显像的国际领先技术,它为临床诊断和治疗提供全新的手段。
(1)PET在心脏疾病诊疗中,需要使用放射正电子的同位素氮13示踪剂,氮13是由小型回旋加速器输出的高速质子轰击氧16获得的,反应中同时还产生另一个粒子,试写出该核反应方程。
(2)PET所用回旋加速器示意如图7.11,其中置于高真空中的金属D形盒的半径为R,两盒间距为d,在左侧D形盒圆心处放有粒子源S,匀强磁场的磁感应强度为B,方向如图所示。质子质量为m,电荷量为q。设质子从粒子源S进入加速电场时的初速度不计,质子在加速器中运动的总时间为t(其中已略去了质子在加速电场中的运动时间),质子在电场中的加速次数于回旋半周的次数相同,加速质子时的电压大小可视为不变。求此加速器所需的高频电源频率f和加速电压U。
(3)试推证当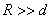 时,质子在电场中加速的总时间相对于在D形盒中回旋的时间可忽略不计(质子在电场中运动时,不考虑磁场的影响)。
时,质子在电场中加速的总时间相对于在D形盒中回旋的时间可忽略不计(质子在电场中运动时,不考虑磁场的影响)。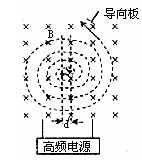
一如图所示,在倾角为θ的光滑斜面上端系一劲度系数为k的轻弹簧,弹簧下端连有一质量为m的小球,球被一垂直于斜面的挡板A挡住,此时弹簧没有形变。若手持挡板A以加速度a(a<gsinθ)沿斜面匀加速下滑,求:
(1)从挡板开始运动到球与挡板分离所经历的时间;
(2)从挡板开始运动到球速达到最大,球所经过的最小路程。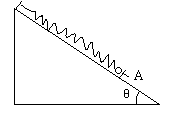
一位同学的家住在一座25层的高楼内,他每天乘电梯上楼,经过多次仔细观察和反复测量,他发现电梯启动后的运动速度符合如图所示的规律,他就根据这一特点在电梯内用台秤、重物和停表测量这座楼房的高度。他将台秤放在电梯内,将重物放在台秤的托盘,电梯从第一层开始启动,经过不间断地运行,最后停在最高层。在整个过程中,他记录了台秤在不同时间段内的示数,记录的数据如下表所示,但由于0~3.0s段的时间太短,他没有来得及将台秤的示数记录下来。假设在每个时间段内台秤的示数都是稳定的,重力加速度g取10m/s2。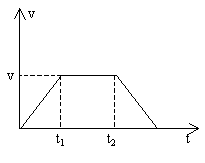
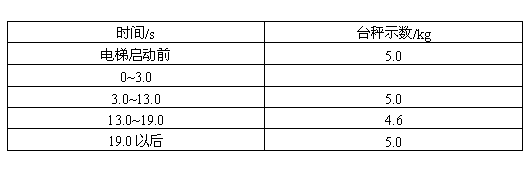
(1)电梯在0~3.0s内台秤的示数应该是多少?
(2)根据测量的数据,计算该座楼房每一层的平均高度。