如图所示，在xoy平面第Ⅰ象限有匀强电场，场强大小未知，其方向沿y轴正向；在第Ⅱ象限有垂直纸面向里的匀强磁场，磁感应强度为B；P处有一放射源，内装放射性物质
，发生衰变生成新核
，放出一个质量为m，电荷量为－q的带电粒子。带电粒子从P孔以初速度v0沿垂直于磁场方向进入匀强磁场中，初速度方向与－x轴的夹角θ=60°，粒子恰好从C孔垂直于y轴射入匀强电场，最后打在Q点，已知OQ=2OC，不计粒子的重力，
（1）写出发生衰变时的核反应方程
（2）求粒子从P运动到Q所用的时间t
（3）求粒子到达Q点的动能EkQ
如图1-6-10所示，平板小车停在光滑水平面上，质量均为m的物块A和B从小车两端相向滑上小车上表面，它们的水平速度大小分别为 2v0和v0.若小车质量为 m，A和B与小车间的动摩擦因数均为μ，试问经过多少时间A和B相对静止？（小车足够长，A、B不相撞）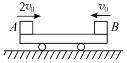
图1-6-10
新的交通法规的颁布和执行，对确保道路畅通，保证人们的生命财产安全，具有十分重要的意义.某平直公路上一质量为m1="1" 200 kg、以速度v1="21" m/s行驶的汽车A，发现在它前方s0="33" m处有一质量为m2="800" kg、以速度v2="15" m/s迎面驶来的汽车B，两车同时急刹车，但由于惯性仍使两车猛烈相撞并结合在一起滑行一段距离后停下.设路面与两车的动摩擦因数μ均为0.3,g取10 m/s2，忽略碰撞过程中路面摩擦力的冲量.设两车的相撞时间（从两车接触到一起滑行）t0="0.02" s,则每个驾驶员受到的水平平均冲力是其自身重力的几倍？
如图1-6-8所示，甲车质量为2 kg，静止在光滑水平面上，上表面光滑，右端放一质量为1 kg的小物体.乙车质量为4 kg，以5 m/s的速度向左运动，与甲车相碰后甲车获得8 m/s 的速度，物体滑到乙车上.若乙车足够长，上表面与物体的动摩擦因数为0.2，则物体在乙车上滑行多长时间相对乙车静止？
图1-6-8
如图 1-6-7 所示，静止在光滑水平面上的小车质量为 M="20" kg.从水枪中喷出的水柱的横截面积为 S="10" m2，速度为 v="10" m/s，水的密度为ρ=1.0×103 kg/m3.若用水枪喷出的水从车后沿水平方向冲击小车的前壁，且冲击到小车前壁的水全部沿前壁流进小车中.当有质量为 m="5" kg 的水进入小车时，试求：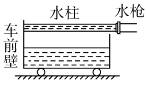
图1-6-7
（1）小车的速度大小；
（2）小车的加速度大小.
一块足够长的木板，放在光滑水平面上.在木板上自左向右放有序号是1、2、3……n的木块，所有木块的质量均为m，与木板间的动摩擦因数都相同.开始时，木板静止不动，第1、2、3……n号木块的初速度分别为v0、2v0、3v0……nv0,v0方向都向右，如下图所示，木板的质量与所有木块的总质量相等，最终所有小木块都与木板以相同的速度匀速运动.求在整个过程中木板运动的最大速度.