质量为m的小球B用一根轻质弹簧连接.现把它们放置在竖直固定的内壁光滑的直圆筒内,平衡时弹簧的压缩量为 ,如图所示,小球A从小球B的正上方距离为3x0的P处自由落下,落在小球B上立刻与小球B粘连在一起向下运动,它们到达最低点后又向上运动,并恰能回到0点(设两个小球直径相等,且远小于
,如图所示,小球A从小球B的正上方距离为3x0的P处自由落下,落在小球B上立刻与小球B粘连在一起向下运动,它们到达最低点后又向上运动,并恰能回到0点(设两个小球直径相等,且远小于 略小于直圆筒内径),已知弹簧的弹性势能为
略小于直圆筒内径),已知弹簧的弹性势能为 ,其中k为弹簧的劲度系数,Δx为弹簧的形变量。求:
,其中k为弹簧的劲度系数,Δx为弹簧的形变量。求:
(1)小球A质量。
(2)小球A与小球B一起向下运动时速度的最大值.
如图13-8-3所示,一水平放置的圆盘绕竖直固定轴转动,在圆盘上沿半径开有一条宽度为2 mm的均匀狭缝.将激光器与传感器上下对准,使二者间连线与转轴平行,分别置于圆盘的上下两侧,且可以同步地沿圆盘半径方向匀速移动,激光器连续向下发射激光束.在圆盘转动过程中,当狭缝经过激光器与传感器之间时,传感器接收到一个激光信号,并将其输入计算机,经处理后画出相应图线.图(a)为该装置示意图,图(b)为所接收的光信号随时间变化的图线,横坐标表示时间,纵坐标表示接收到的激光信号强度,图中Δt1=1.0×10-3 s,Δt2=0.8×10-3 s.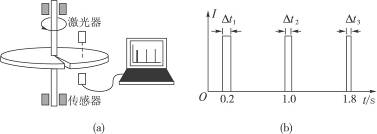
图13-8-3
(1)利用图(b)中的数据求1 s时圆盘转动的角速度;
(2)说明激光器和传感器沿半径移动的方向;
(3)求图(b)中第三个激光信号的宽度Δt3.
天文学家测得银河系中氦的含量约为25%.有关研究表明,宇宙中氦生成的途径有两条:一是在宇宙诞生后2分钟左右生成的;二是在宇宙演化到恒星诞生后,由恒星内部的氢核聚变反应生成的.
(1)把氢核聚变反应简化为4个氢核 聚变成氦核
聚变成氦核 ,同时放出两个正电子
,同时放出两个正电子 和2个中微子(ν0),请写出氢核聚变反应的方程,并计算一次反应释放的能量;
和2个中微子(ν0),请写出氢核聚变反应的方程,并计算一次反应释放的能量;
(2)研究表明,银河系的年龄约为t=3.8×1017 s,每秒钟银河系产生的能量约为1×1037 J(即P=1×1037 J/s).现假定该能量全部来自上述氢核聚变反应,试估算银河系中氦的含量(最后结果保留一位有效数字);
(3)根据你的估算结果,对银河系中氦的主要生成途径作出判断.
(可能用到的数据:银河系质量约为M=3×1041 kg,原子质量单位1 u=1.66×10-27kg,1 u相当于1.5×10-10 J的能量,电子质量me=0.000 5 u,氦核质量mα=4.002 6 u,氢核质量mH=1.007 8 u,中微子质量为零)
太阳内部进行着剧烈的氢核聚变反应,氦核是由4个质子生成,同时有正电子放出,正电子又会和负电子湮没成为一对光子,在这一核反应过程中放出4.5×10-12 J能量,已知现在太阳每秒辐射5.0×1026 J能量.
(1)写出上述两个核反应方程;
(2)计算出太阳每秒产生的氦核数目及每年减少的质量.(保留两位有效数字)
已知氘核质量为2.013 6 u,中子质量为1.008 7 u, He核的质量为3.015 0 u;
He核的质量为3.015 0 u;
(1)写出两个氘核聚变成 He核反应方程;
He核反应方程;
(2)计算上述核反应中释放的核能;
(3)若两个氘核以相等的动能0.35 MeV作对心碰撞即可发生上述核反应,其释放的核能全部转化为机械能,则反应中生成的 He核和中子的动能各是多少?
He核和中子的动能各是多少?
已知氘核的质量为2.013 6 u,中子的质量为1.008 7 u, 的质量为3.015 0 u.
的质量为3.015 0 u.
(1)写出两个氘核聚变成 的核反应方程;
的核反应方程;
(2)计算上述核反应中释放的核能;
(3)若两氘核以相等的动能0.35 MeV做对心碰撞,即可发生上述核反应,且释放的核能全部转化为机械能,则反应中生成的32He核和中子的动能各是多少?