已知 ,
, 是纯虚数,又
是纯虚数,又 ,求
,求 .
.
数列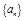 的前
的前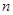 项和为
项和为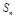 ,
,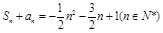 .
.
(Ⅰ)设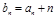 ,证明:数列
,证明:数列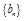 是等比数列;
是等比数列;
(Ⅱ)求数列 的前
的前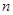 项和
项和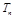 .
.
(Ⅲ)若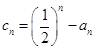 ,
,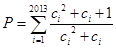 ,求不超过
,求不超过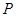 的最大的整数值.
的最大的整数值.
甲、乙两人进行围棋比赛,规定每局胜者得1分,负者得0分,比赛进行到有一方比对方多2分或打满6局时停止.设甲在每局中获胜的概率为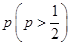 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为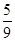 .
.
(Ⅰ)求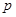 的值;
的值;
(Ⅱ)设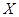 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量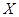 的分布列和数学期望
的分布列和数学期望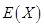 .
.
已知函数 ,
, .
.
(Ⅰ)求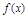 的极值;
的极值;
(Ⅱ)当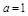 时,若不等式
时,若不等式 在
在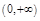 上恒成立,求
上恒成立,求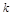 的取值范围.
的取值范围.
如图,在三棱锥 中,
中, ,
,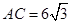 ,
,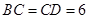 ,设顶点A在底面
,设顶点A在底面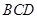 上的射影为R.
上的射影为R.
(Ⅰ)求证: 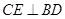 ;
;
(Ⅱ)设点 在棱
在棱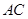 上,且
上,且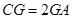 ,试求二面角
,试求二面角 的余弦值.
的余弦值.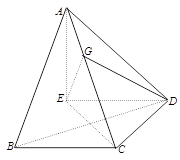
在△ABC中,已知 ,其中
,其中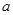 、
、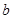 、
、 分别为
分别为 的内角
的内角 、
、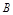 、
、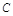 所对的边.求:
所对的边.求:
(Ⅰ)求角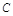 的大小;
的大小;
(Ⅱ)求满足不等式 的角
的角 的取值范围.
的取值范围.