甲、乙两人进行围棋比赛,规定每局胜者得1分,负者得0分,比赛进行到有一方比对方多2分或打满6局时停止.设甲在每局中获胜的概率为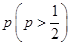 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为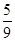 .
.
(Ⅰ)求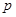 的值;
的值;
(Ⅱ)设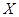 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量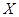 的分布列和数学期望
的分布列和数学期望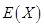 .
.
如果实数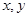 满足
满足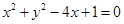 求:
求:
(1)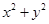 的最值;
的最值;
(2)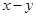 的最大值.
的最大值.
已知全集 ,集合
,集合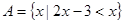 ,集合
,集合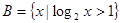 ;
;
(1)求集合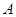 、
、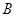 ; (2)求
; (2)求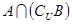 .
.
已知函数 ,在
,在 时取得极值.
时取得极值.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若 时,
时, 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(Ⅲ)若 ,是否存在实数b,使得方程
,是否存在实数b,使得方程 在区间
在区间 上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
在数列 中,
中,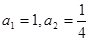 ,且
,且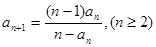 .
.
(Ⅰ) 求 ,猜想
,猜想 的表达式,并加以证明;
的表达式,并加以证明;
(Ⅱ)设 ,求证:对任意的自然数
,求证:对任意的自然数 都有
都有 .
.
某车间有50名工人,要完成150件产品的生产任务,每件产品由3个A 型零件和1个B 型零件配套组成.每个工人每小时能加工5个A 型零件或者3个B 型零件,现在把这些工人分成两组同时工作(分组后人数不再进行调整),每组加工同一中型号的零件.设加工A 型零件的工人人数为x名(x∈N*)
(1)设完成A 型零件加工所需时间为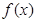 小时,写出
小时,写出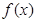 的解析式;
的解析式;
(2)为了在最短时间内完成全部生产任务,x应取何值?