⑴匀强电场的场强E;
⑵AD之间的水平距离d;
⑶已知小颗粒在轨迹DP上某处的最大速度为vm,该处轨迹的
曲率半径是距水平面高度的k倍,则该处的高度为多大?
水平平行放置的两根长直光滑金属导轨MN与PQ上放有一根直导线ab,ab与导轨垂直,其电阻为0.02 ,质量为0.1kg,它在导轨间的长度为20cm,导轨处于方向竖直向下的匀强磁场中,B=0.2T,电路中电阻R=0.008
,质量为0.1kg,它在导轨间的长度为20cm,导轨处于方向竖直向下的匀强磁场中,B=0.2T,电路中电阻R=0.008 ,其它电阻不计,求:
,其它电阻不计,求:
(1)断开电键K,ab在水平恒力F=0.1N的作用下,由静止开始沿轨道滑动过程中ab中的电动势随时间变化的表达式.
(2)当ab以10m/s的速度滑动时,闭合电键,并同时撤掉F力,那么由此时开始以后的时间里电路中电阻R放出焦耳热是多少.
如图,所示,光滑的金属导轨ad与bc与两个定值电阻R1、R2相连组成闭合的矩形导体框,导体框水平放置,金属棒ef与ad及bc边垂直并接触良好,空间存在着方向竖直向下的匀强磁场,磁感强度为B,已知电阻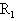 =R;
=R; =4R,其它部分电阻忽略不计,ad与bc相距为L,给ef施加一个与之垂直的水平恒力F,求:①ef棒做匀速运动时的速度是多大?②当ef棒做匀速运动时,电阻R2消耗的电功率多大?
=4R,其它部分电阻忽略不计,ad与bc相距为L,给ef施加一个与之垂直的水平恒力F,求:①ef棒做匀速运动时的速度是多大?②当ef棒做匀速运动时,电阻R2消耗的电功率多大?
如图所示,在两条平行光滑导轨上,垂直放着导体杆ab,导轨和杆的电阻忽略不计,匀强磁场方向与导轨平面垂直,导轨左侧接有如图示电路,已知电阻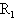 =5.0Ω,
=5.0Ω,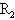 =6.0Ω,电压表量程为0—10V,电流表量程为0—3A,其内阻对电路影响不计。现将变阻器电阻调为30Ω,同时ab杆受F=4.0N的水平拉力沿导轨向右做匀速直线运动,这时两表中恰有一表满量程,另一表可安全使用,求ab杆速度的大小?
=6.0Ω,电压表量程为0—10V,电流表量程为0—3A,其内阻对电路影响不计。现将变阻器电阻调为30Ω,同时ab杆受F=4.0N的水平拉力沿导轨向右做匀速直线运动,这时两表中恰有一表满量程,另一表可安全使用,求ab杆速度的大小?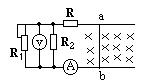
如图MN为金属杆,在竖直平面内贴着光滑金属平行导轨下滑,导轨间距L=10cm,导轨上端接有电阻R=0.5Ω,导轨与金属杆电阻不计,整个装置处于B=0.5T的与纸面垂直的水平匀强磁场中,已知杆稳定下落时,每秒钟有0.02J的重力势能转化为电能,求杆稳定下落的速度有多大?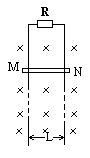
如图所示,abcd是由粗裸铜导线连接两个定值电阻组成的闭合矩形导体框,水平放置,金属棒ef与ab及cd边垂直,并接触良好,空间存在着匀强磁场,磁感强度大小为B,方向竖直向下,已知电阻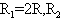 =3R,其它部分的电阻都可忽略不计,ab及cd边相距为L.给ef棒施加一个跟棒垂直的恒力F,
=3R,其它部分的电阻都可忽略不计,ab及cd边相距为L.给ef棒施加一个跟棒垂直的恒力F,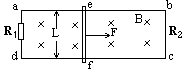
(1)ef棒做匀速运动时的速度是多大?
(2)当ef棒做匀速运动时,电阻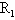 消耗的电功率多大?
消耗的电功率多大?